初中 数学
计算4﹣1的结果为( )
A . ﹣4
B . ﹣  C . 4
D .
C . 4
D . 
 C . 4
D .
C . 4
D . 
诺如病毒的直径大约0.0000005米,将0.0000005用科学记数法可表示为
如图,边长为1的正六边形ABCDEF放置于平面直角坐标系中,边AB在x轴正半轴上,顶点F在y轴正半轴上,将正六边形ABCDEF绕坐标原点O顺时针旋转,每次旋转60°,那么经过第2025次旋转后,顶点D的坐标为( )

A . (  ,
,  )
B . (
)
B . (  ,
,  )
C . (
)
C . (  ,
,  )
D . (
)
D . (  ,
,  )
)
 ,
,  )
B . (
)
B . (  ,
,  )
C . (
)
C . (  ,
,  )
D . (
)
D . (  ,
,  )
)
已知线段QP,AP=AQ,以QP为直径作圆,点A与此圆的位置关系是( )
A . 点A在圆内
B . 点A在圆上
C . 点A在圆外
D . 不能确定
据统计,2022年湖南省湘西土家族苗族自治州学业水平考试九年级考生报名人数约为35000人,其中数据35000用科学记数法表示为( )
A . 35×103
B . 0.35×105
C . 350×102
D . 3.5×104
某工人计划加工一批产品,如果每小时加工产品10个,就可以在预定时间完成任务,如果每小时多加工2个,就可以提前1小时完成任务.
-
(1) 该产品的预定加工时间为几小时?
-
(2) 若该产品销售时的标价为100元/个,按标价的八折销售时,每个仍可以盈利25元,该批产品总成本为多少元?
若式子  有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A . 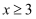 B .
B .  C .
C . 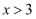 D .
D . 
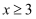 B .
B .  C .
C . 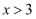 D .
D . 
在△ABC中,已知AB=5,BC=6,∠B=30°,那么S△ABC为( ).
A . 7.5
B . 15
C . 30
D . 60
已知  和
和  是同类项,则
是同类项,则  的值是( )
的值是( )
 和
和  是同类项,则
是同类项,则  的值是( )
的值是( )
A . 6
B . 4
C . 3
D . 2
不等式1﹣x>0的解集在数轴上表示正确的是( )
A . 
B .
B .  C .
C . 
D .
D . 

B .
B .  C .
C . 
D .
D . 
 的倒数是( ).
的倒数是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在水果销售旺季,某水果店购进一种优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足的关系为一次函数  .
.
 .
.
-
(1) 某天这种水果的售价为23.5元/千克,求当天该水果的销售量;
-
(2) 如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如下表所示:
选手 | 甲 | 乙 | 丙 | 丁 |
方差 | 0.035 | 0.036 | 0.028 | 0.015 |
则这四人中成绩最稳定的是( )
A . 甲
B . 乙
C . 丙
D . 丁
若|a﹣2|+(b+0.5)2=0,则a11b11=.
-27的立方根为( )
A .  B .
B .  C . -3
D . 3
C . -3
D . 3
 B .
B .  C . -3
D . 3
C . -3
D . 3
如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )

A . 147°
B . 108°
C . 105°
D . 以上答案都不对
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为 ( )
A.30° B.36° C.40° D.45°
 |
如图,直线![]() 与x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点
与x、y轴分别交于点A、B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点![]() 恰好落在直线AB上,则点C的坐标为 .
恰好落在直线AB上,则点C的坐标为 .

.用反证法证明真命题“四边形中至少有一个角不小于90°”时,应假设( )
A.四边形中没有一个角不小于90°
B.四边形中至少有两个角不小于90°
C.四边形中四个角都不小于90°
D.四边形中至多有一个角不小于90°
最近更新
- 小明用刻度尺测物体的长度,如图所示,他所用的刻度尺的分度值是__________,物体的长度是__________.
- 在一固定体积的密闭容器中,可逆反应nA(g)+mB(g)pC(g)(正反应放热,n+m>p)已经达到平衡状态。下列分析结
- 生命活动离不开细胞,不包括下列内容中的( )A.膝跳反射的完成是以细胞为结构基础B.生态系统中的物质和能量交换以细胞
- 《诗经》云:“雨我公田,遂及我私”。这种现象开始出现于( ) A.商朝 B.西周 C.
- 备受关注的《国有土地房屋征收与补偿条例(征求意见稿)》于2010年1月29日向公众征求意见。这表明,公民可以通过
- 小青对正在抽烟的爸爸说:“吸烟不但危害你的健康,我和妈妈也在被动吸烟.”小青这样认为的科学依据是:A. 分子很小;
- 某鱼雷采用Al-AgO动力电池,以溶解有氢氧化钾的流动海水为电解液,电池反应为:2Al+3AgO+2KOH3Ag+2KA
- 读俄罗斯与澳大利亚两国自然地理分布简图,回答下列问题。(14分) (1)俄罗斯自然地理分布图中,图例A、B、C所表
- Do you know when and where the first republic ______ ? A. tu
- . 已知,试证明至少有一个不小于1.
- Britain’s parents have admitted school is harder today than
- 水稻的基因型为Aa,自交2次,后代中的纯合体占总数的() A.25% B.50% C.75% D.100%
- (本题6分)如图,直线AG交□ABCD的对角线BD于点E,交BC于点F,交DC的延长线于G.(1)请找出一个与△ADG相
- 下表为四种农作物产销资料,假如该地区是一个地势平坦的平原,可种植花卉、蔬菜、稻米和甘蔗等四种农作物,其产品全部提供某一市
- ______untidily and speaking in a strange way, father must ha
- 阅读下面的文字,完成下列各题。 人与生物圈计划 人与生物圈计划中国有,世界其他国家也有。目的是寻求同一个答案。为什么人们
- 直线的倾斜角是
- 下列各组中的反应,属于同一反应类型的是( )A.由溴乙烷水解制乙醇;由乙烯与水反应制乙醇 B.由甲苯硝化制TNT
- ......
- 读下图,完成22,23题。22.该地河流夏季进入汛期,原因是( ) A.处于季风区,夏季降水多



