初中 数学
正方形  中,
中,  、
、  分别是
分别是  、
、  上的动点,且
上的动点,且 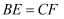 ,
,  与
与 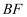 交于点
交于点  .
.
 中,
中,  、
、  分别是
分别是  、
、  上的动点,且
上的动点,且 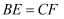 ,
,  与
与 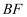 交于点
交于点  .
. 
-
(1) 如图1,若
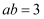 ,
,  ,求
,求  ;
;
-
(2) 如图2,在
 上截取
上截取  ,
,  的平分线交
的平分线交 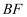 于点
于点  ,连接
,连接  ,求证:
,求证:  .
.
-
(3) 如图3,若
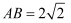 ,在
,在  上截取
上截取  ,点
,点  、
、  分别是
分别是  、
、  上的动点,直接写出
上的动点,直接写出  的周长的最小值.
的周长的最小值.
下列因式分解正确的是( )
A . x2+2x﹣1=(x﹣1)2
B . x2+1=(x+1)2
C . 2x2﹣2=2(x+1)(x﹣1)
D . x2﹣x+1=x(x﹣1)+1
计算:
-
(1) (﹣1)2020+(﹣
 )﹣2﹣(3.14﹣π)0;
)﹣2﹣(3.14﹣π)0;
-
(2) 先化简,再求值:[(a﹣b)2﹣(a﹣2b)(2a+5b)+(a+b)(a﹣b)]÷2b , 其中a=1,
 .
.
如图所示,在菱形ABCD中,AB=6,∠BAD=120°,点E,F分别在菱形的边BC,CD上滑动,满足∠EAF=60°,连接EF,且E,F不与B,C,D重合.

-
(1) 求证:不论E,F在BC,CD上如何滑动,总有BE=CF;
-
(2) 当点E,F在BC,CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
实数2,0,-2,  中,最大的数是( )
中,最大的数是( )
 中,最大的数是( )
中,最大的数是( )
A . 2
B . 0
C . -2
D . 

在平面直角坐标系xOy中,⊙O的半径为1,对于⊙O和⊙O外的点P,给出如下的定义:若在  上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为⊙O的近距点.
上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为⊙O的近距点.
 上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为⊙O的近距点.
上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为⊙O的近距点. 
-
(1) 在点
 ,
,  ,
,  ,
,  中,⊙O的近距点是.
中,⊙O的近距点是.
-
(2) 若直线
 上存在⊙O的近距点,求b的取值范围;
上存在⊙O的近距点,求b的取值范围;
-
(3) 若点P在直线
 上,且点P是⊙O的近距点,求点P横坐标
上,且点P是⊙O的近距点,求点P横坐标  的取值范围.
的取值范围.
如图,正方形  的边长是
的边长是  ,
,  是
是  上一点,
上一点,  是
是  延长线上的一点,
延长线上的一点,  .四边形
.四边形  是矩形,矩形
是矩形,矩形  的面积
的面积  与
与  的长
的长 
 的函数关系是.
的函数关系是.
 的边长是
的边长是  ,
,  是
是  上一点,
上一点,  是
是  延长线上的一点,
延长线上的一点,  .四边形
.四边形  是矩形,矩形
是矩形,矩形  的面积
的面积  与
与  的长
的长 
 的函数关系是.
的函数关系是. 
计算题:(2a+3b)(2a﹣3b)﹣(a﹣3b)2=.
小颖用几何画板软件探索方程ax2+bx+c=0的实数根,作出了如图所示的图象,观察得一个近似根为x1=﹣4.5,则方程的另一个近似根为x2= (精确到0.1).

若关于  一元二次方程
一元二次方程  不含一次项,则
不含一次项,则  .
.
 一元二次方程
一元二次方程  不含一次项,则
不含一次项,则  .
.
先化简,再求值:x2(x+1)﹣x(x2+x﹣1),其中x=  ﹣1.
﹣1.
 ﹣1.
﹣1.
如图,等边 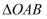 的边
的边  在
在  轴的负半轴上,双曲线
轴的负半轴上,双曲线  过
过  的中点,已知等边三角形的边长是
的中点,已知等边三角形的边长是  ,则该双曲线的表达式为( )
,则该双曲线的表达式为( )
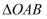 的边
的边  在
在  轴的负半轴上,双曲线
轴的负半轴上,双曲线  过
过  的中点,已知等边三角形的边长是
的中点,已知等边三角形的边长是  ,则该双曲线的表达式为( )
,则该双曲线的表达式为( ) 
A . 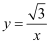 B .
B .  C .
C .  D .
D . 
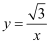 B .
B .  C .
C .  D .
D . 
如图在梯形ABCD中,AD∥BC,AD⊥CD,BC=CD=2AD,E是CD上一点,∠ABE=45°,则tan∠AEB的值等于( )

A . 3
B . 2
C .  D .
D . 
 D .
D . 
如图,在 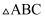 中,D是BC边上一点,
中,D是BC边上一点,  ,
,  ,求
,求  的度数.
的度数.
 中,D是BC边上一点,
中,D是BC边上一点,  ,
,  ,求
,求  的度数.
的度数. 
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG= ,则△EFC的面积是( )
,则△EFC的面积是( )

 ,则△EFC的面积是( )
,则△EFC的面积是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列关于x的方程中,一定是一元二次方程的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫格点,顶点在格点的四边形称为格点四边形.已知A,B,P均为格点,请在给定的网格中按要求画出格点平行四边形,且点P不与其它顶点重合。

-
(1) 在图甲中画一个以AB为边,且其邻边经过点P的平行四边形ABCD。
-
(2) 在图乙中画一个以AB为对角线,且另一条对角线经过点P的平行四边形AEBF。
定义新运算:对于任意有理数a、b都有a⊗b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算.比如:2⊗5=2×(2﹣5)+1=2×(3)+1=6+1=5.则4⊗x=13,则x=.
如图,已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(5,0)、C(0,﹣5)三点.

-
(1) 求抛物线的解析式和顶点坐标;
-
(2) 当0<x<5时,y的取值范围为;
-
(3) 点P为抛物线上一点,若S△PAB=21,直接写出点P的坐标.
若等式![]() 对任意的x(
对任意的x(![]() )恒成立,则
)恒成立,则![]() ( )
( )
A、8 ![]() 、-8 C、16 D、-16
、-8 C、16 D、-16
最近更新
- 餐厅的服务员用盖子熄灭酒精炉,该灭火方法的主要原理是 A. 隔绝空气 B.降低温
- 工业废水中常含有一定量的Cr2O72-和CrO42-,它们会对人类及生态系统产生很大的伤害,必须进行处理。某工厂使用还原
- 20世纪70年代中美关系改善的根本原因是 A.中国国际影响的扩大 B.双
- 中国历史上的第一个统一的中央集权的封建王朝建立于公元前 A.2世纪早期 B.2世纪晚期C
- All that shines ______ not gold. A. has B. have C. is
- 下列反应中属于取代反应的是 ① CH3CH=CH2+Br2CH3CHBrCH2Br② CH3CH2OHCH2=CH2+
- 室温下,水的电离达到平衡:H2OH++OH-。下列叙述正确的是() A.将水加热,平衡向正反应方向移动,KW不变 B.向
- 2010年1月2日起,我国北方大部地区遭遇大范围降雪天气袭击。大雪严重影响了民航、铁路和高速公路等交通,如图所示。在遇
- Eliza remembers everything exactlyas if it________yesterday.
- 下列函数中,周期为,且在上为减函数的是 A. B. C. D.
- Fitness First Initiative for Teenagers(FFIT)is a plan from F
- Now then, children, Its time you ________. A. were washed an
- 3.依次填入下面一段文字横线处的语句,衔接最恰当的一组是( )茫茫沙漠,滔滔流水,于世无奇。惟有大漠中如此一湾,
- 弱电解质的电离程度可用电离度()表示:,现有pH均为4的HCl和溶液,则两种溶液中H2O的电离度之比为()A、1:2
- (9分)经检测汽车A的制动性能:以标准速度20m/s在平直公路上行使时,制动后40s停下来。现A在平直公路上以20m/s
- 据温商网报道:2010年1月27日,以“改善世界现状重新思考,重新设计,重新构建”为主题的达沃斯世界经济论坛开幕。WTO
- 下列物质的水溶液经加热浓缩,蒸干灼烧仍能得到原物质的是A.FeCl3 B.Ca(HCO3)2
- 甲乙两个质点间的万有引力大小为F,若甲物体的质量不变,乙物体的质量增加到原的2倍,同时,它们之间的距离减为原的1/2,则
- 如图为细胞分裂过程示意图,据图分析不能得出() A. 如图所示细胞分裂过程中,DNA复制发生了三次
- 从所给句子中选择恰当的一项完成对话,有两个句子是多余的 A.It’s Kay. B.Nice to see



