初中 数学
如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
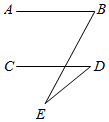
A . 20°
B . 30°
C . 50°
D . 70°
直角坐标系中,点P(2,5)所在的象限是( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
如图,点P是∠AOB平分线OC上一点,PD⊥OB , 垂足为D , 若PD=2,则点P到边OA的距离是.

下列事件中,是必然事件的是( )
A . 在地球上,上抛出去的篮球会下落
B . 打开电视机,任选一个频道,正在播新闻
C . 任意买一张电影票,座位号是偶数
D . 三根长度为2cm,2cm,4cm的木棒首尾顺次相接能摆成三角形
在△ABC中,∠ACB=90°,AC=BC,点D在AC边上(不与点A,C重合),连接BD,过点D作DE⊥BD,点E与点A在直线BC的两侧,DE=BD,延长BC至点F,使CF=BC,连接EF.


-
(1) 依题意补全图1;
-
(2) 在点A,B,C,D中,和点F所连线段与DE相等的是点.
①求∠CFE的度数;
②连接EC并延长,交AB于点M,用等式表示线段EC与MC之间的数量关系,并证明.
星城长沙是湖南省省会城市,也是长江中游地区重要的中心城市,以下能准确表示长沙地理位置的是( )
A . 在北京的西南方
B . 东经112.59°,北纬28.12°
C . 距离北京1478千米处
D . 东经112.59°
已知二次函数  (其中
(其中  为常数),该函数图象与
为常数),该函数图象与  轴交点在
轴交点在  轴上方,则
轴上方,则  的取值范围正确的是( )
的取值范围正确的是( )
 (其中
(其中  为常数),该函数图象与
为常数),该函数图象与  轴交点在
轴交点在  轴上方,则
轴上方,则  的取值范围正确的是( )
的取值范围正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在﹣1.414,  ,π,3.14,2+
,π,3.14,2+ 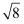 ,3.212212221…(两个1之间依次多一个2),这些数中,无理数的个数为( )
,3.212212221…(两个1之间依次多一个2),这些数中,无理数的个数为( )
 ,π,3.14,2+
,π,3.14,2+ 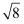 ,3.212212221…(两个1之间依次多一个2),这些数中,无理数的个数为( )
,3.212212221…(两个1之间依次多一个2),这些数中,无理数的个数为( )
A . 5
B . 2
C . 3
D . 4
如图,在△ABC中,AB=AC , ∠CAB=α , 分别以AB , BC为边在BC同侧作等边△ABD和等边△BCE , 连接AE , DC .

-
(1) 求∠ACE的度数(用α表示);
-
(2) 求证:AE平分∠BAC;
-
(3) 若BF⊥CD , 交DC的延长线于点F , 当△BCF的面积为
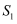 ,△BCE的面积为
,△BCE的面积为  ,求
,求 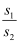 的值.
的值.
如图,点A,B,C是⊙O上的点,且∠ACB=40°,阴影部分的面积为8π,则此扇形的半径为( )

A . 3
B . 4
C . 5
D . 6
时下娱乐综艺节目风靡全国,随机对九年级部分学生进行了一次调查,对最喜欢《我是喜剧王》(记为A)、《王牌对王牌》(记为B)、《奔跑吧,兄弟》(记为C)、《欢乐喜剧人》(记为D)的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:

-
(1) 求本次调查一共选取了多少名学生;
-
(2) 将条形统计图补充完整;
-
(3) 若九年级共有1900名学生,估计其中最喜欢《奔跑吧,兄弟》的学生大约是多少名.
如图,将二次函数  的图像沿
的图像沿  轴对折,得到的新的二次函数的表达式是( )
轴对折,得到的新的二次函数的表达式是( )
 的图像沿
的图像沿  轴对折,得到的新的二次函数的表达式是( )
轴对折,得到的新的二次函数的表达式是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在一个袋子里装有10个球,6个红球,3个黄球,1个绿球,这些球除颜色外、形状、大小、质地等都完全相同,充分搅匀后,在看不到球的条件下,随机从这个袋子中摸出一球,摸出红球的概率是.
当x=时,分式  的值为0.
的值为0.
 的值为0.
的值为0.
如图,已知反比例函数 的图象经过点
的图象经过点 , 过A作AC⊥y轴于点C.点B为反比例函数图象上的一动点,过点B作BD⊥x轴于点D,直线BC与x轴的负半轴交于点E.
, 过A作AC⊥y轴于点C.点B为反比例函数图象上的一动点,过点B作BD⊥x轴于点D,直线BC与x轴的负半轴交于点E.
 的图象经过点
的图象经过点 , 过A作AC⊥y轴于点C.点B为反比例函数图象上的一动点,过点B作BD⊥x轴于点D,直线BC与x轴的负半轴交于点E.
, 过A作AC⊥y轴于点C.点B为反比例函数图象上的一动点,过点B作BD⊥x轴于点D,直线BC与x轴的负半轴交于点E.
-
(1) 求反比例函数的表达式;
-
(2) 若BD=3OC,求△BDE的面积.
如图,  是反比例函数
是反比例函数  的图象上一点,过点
的图象上一点,过点  作
作  轴交反比例函数
轴交反比例函数  的图象于点
的图象于点  ,已知
,已知 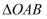 的面积为
的面积为  ,则
,则  的值为.
的值为.
 是反比例函数
是反比例函数  的图象上一点,过点
的图象上一点,过点  作
作  轴交反比例函数
轴交反比例函数  的图象于点
的图象于点  ,已知
,已知 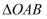 的面积为
的面积为  ,则
,则  的值为.
的值为.

如果函数![]() ,那么
,那么![]()
点P(![]() a+5,a-2)在x轴上,则P点坐标为 。
a+5,a-2)在x轴上,则P点坐标为 。
在数轴上表示数:-2,![]() .按从小到大的顺序用"<"连接起来.
.按从小到大的顺序用"<"连接起来.
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
(1)写出y与t之间的函数关系式;
(2)通话2分钟应付通话费多少元?通话7分钟呢?

最近更新
- 具备基本的化学实验技能是进行科学探究的基础和保证。下列实验装置或操作正确的是
- 阅读下面一首宋词,完成13――14题卜算子・ 片片蝶衣轻(南宋)刘克庄 片片蝶衣轻,点点猩红小。 道是天
- You______a newfriend. If you have a friend, you get happines
- 下面一些角中,可以用一副三角尺画出来的角是( ) (1)15°的角, (2)65º的角, (3)75º的角,
- 请阅读晏殊的《浣溪沙》回答问题,(3)、(4)两个小题中可任选一题作答,若全对可加1分。(3分) 一曲新词酒一杯, 去年
- 已知函数对一切x∈R,f(x)+f(1-x)=1.求f(0)+f+f+…++
- 下列说法,不正确的一项是() A.“庐陵萧君圭君玉”一句中,“君圭”是名,“君玉”是字。 B.“至和元年七月某日”一
- Everymorning I try _____, but I’m still late sometimes. A.
- 图8中电能表的示数是______kWh
- 斯大林在《宗教改革和伟大农民战争时期的德国》一文中写道:教皇在特使报告中说:“十分之九的德国人高喊:‘路德’;剩下的十分
- 假日,小强在广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC的长为10米,小强的
- 甲酵母菌进行了有氧呼吸,乙酵母菌进行了酒精发酵,若它们消耗了等量的葡萄糖,则甲吸入的氧气和它们放出的二氧化碳的体积之比是
- 根据下边的概念图可知,下列叙述正确的是 ( )A.A表示的碱基有5种 B.D表示脱氧
- 下列叙述正确的是 A.
- 下列事实中,不能用勒夏特列原理解释的是 ( ) A.对熟石灰的悬浊液加热,悬浊液中固体质量增加 B.实验室中常用排饱和
- 已知函数 (1)求函数的单调递增区间; (2)若,的值.
- _____ is known to all, China will be an_______ and powerful
- 漫画《设局》告诉我们A.市场调节具有盲目性、滞后性特征 B.社会信用制度要以法律为支撑 C.要遵循市场交易的诚信原则
- 2009年葡萄酒烈酒品鉴会于7月7日在北京兆龙饭店拉开帷幕。在众多媒体、知名酒店与各地葡萄酒经销商的参与下成功举行。我们
- 单词拼写 根据句义完成句中已给出首字母的单词。将每个完整的单词写在各小题右边的横 线上。 1.Han Mei was o



