初中 数学
如图,在△ABC中,CD平分∠ACB,DE∥AC,∠B=50° , ∠EDC=40°,求∠ADC.

我县某中学开展“庆十一”爱国知识竞赛活动,九年级(1)、(2)班各选出  名选手参加比赛,两个班选出的
名选手参加比赛,两个班选出的  名选手的比赛成绩(满分为100分)如图所示。
名选手的比赛成绩(满分为100分)如图所示。
 名选手参加比赛,两个班选出的
名选手参加比赛,两个班选出的  名选手的比赛成绩(满分为100分)如图所示。
名选手的比赛成绩(满分为100分)如图所示。 
-
(1) 根据图示填写如表:
班级
中位数(分)
众数(分)
九(1)
85
九(2)
80
-
(2) 请你计算九(1)和九(2)班的平均成绩各是多少分。
-
(3) 结合两班竞赛成绩的平均数和中位数,分析哪个班级的竞赛成绩较好
-
(4) 请计算九(1)、九(2)班的竞赛成绩的方差,并说明哪个班的成绩比较稳定?
已知一元二次方程2x2+x+m=0的一个根是1,则m的值是.
为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:

-
(1) 本次调查共抽取了多少名学生?
-
(2) 通过计算补全条形统计图;
-
(3) 若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?
如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )

A . 9
B . 7
C . 11
D . 8
数学兴趣小组开展以下折纸活动:先对折矩形  (已知
(已知  ,
,  ),使
),使  和
和  重合,得到折痕
重合,得到折痕  ,把纸片展平;再一次折叠纸片,使点
,把纸片展平;再一次折叠纸片,使点  落在
落在  上,并使折痕经过点
上,并使折痕经过点  ,得到折痕
,得到折痕  ,同时得到线段
,同时得到线段  ,延长
,延长  交
交  于点
于点  .同学们通过观察、探究、计算得到下列结论:①
.同学们通过观察、探究、计算得到下列结论:①  ,②
,②  是等边三角形,③
是等边三角形,③  ,④
,④  .其中正确的结论的序号是.
.其中正确的结论的序号是.
 (已知
(已知  ,
,  ),使
),使  和
和  重合,得到折痕
重合,得到折痕  ,把纸片展平;再一次折叠纸片,使点
,把纸片展平;再一次折叠纸片,使点  落在
落在  上,并使折痕经过点
上,并使折痕经过点  ,得到折痕
,得到折痕  ,同时得到线段
,同时得到线段  ,延长
,延长  交
交  于点
于点  .同学们通过观察、探究、计算得到下列结论:①
.同学们通过观察、探究、计算得到下列结论:①  ,②
,②  是等边三角形,③
是等边三角形,③  ,④
,④  .其中正确的结论的序号是.
.其中正确的结论的序号是. 
如图,在  中,
中,  ,D在边AC上,且
,D在边AC上,且  .
.
 中,
中,  ,D在边AC上,且
,D在边AC上,且  .
. 
-
(1) 如图1,填空

 ,
, 

-
(2) 如图2,若M为线段AC上的点,过M作直线
 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.  求证:
求证:  是等腰三角形;
是等腰三角形; 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.
﹣ 的绝对值为( )
的绝对值为( )
 的绝对值为( )
的绝对值为( )
A . -2
B . - C .
C .  D . 1
D . 1
 C .
C .  D . 1
D . 1
如图,直线  相交于点
相交于点  ,
,  于点
于点  ,且
,且  ,则
,则  为.
为.
 相交于点
相交于点  ,
,  于点
于点  ,且
,且  ,则
,则  为.
为. 
等腰三角形一边长是10cm,一边长是6cm,则它的周长是cm或cm.
已知:一次函数的图象经过点A( 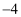 ,
,  )和B(
)和B(  ,
,  ).
).
 ,
,  )和B(
)和B(  ,
,  ).
).
-
(1) 求这个一次函数的表达式;
-
(2) 求这个一次函数与x轴、y轴的交点坐标.
如图所示的几何体由5个大小相同的小立方块组成,它的左视图为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
4的倒数的相反数是( )
A . ﹣4
B . 4
C . -  D .
D . 
 D .
D . 
如果 , 那么
, 那么 的值是.
的值是.
 , 那么
, 那么 的值是.
的值是.
已知 , 若
, 若 , 则
, 则 .
.
 , 若
, 若 , 则
, 则 .
.
我们已知学过完全平方公式 , 知道所有的非负数都可以看作一个数的平方,如
, 知道所有的非负数都可以看作一个数的平方,如 等,那么,我们可以利用这种思想方法和完全平方公式来计算下面的题:
等,那么,我们可以利用这种思想方法和完全平方公式来计算下面的题:
 , 知道所有的非负数都可以看作一个数的平方,如
, 知道所有的非负数都可以看作一个数的平方,如 等,那么,我们可以利用这种思想方法和完全平方公式来计算下面的题:
等,那么,我们可以利用这种思想方法和完全平方公式来计算下面的题:例:求 的算术平方根.
的算术平方根.
解: =
= , 所以
, 所以 的算术平方根是
的算术平方根是 . 你看明白了吗?请根据上面的方法解答下列问题:
. 你看明白了吗?请根据上面的方法解答下列问题:
-
(1) 填空:
 =;
=; =;
=; -
(2) 化简:
 +
+ +
+ +
+ +
+ .
.
如图,点B,O,D在同一直线上,若∠1=15°,∠2=105°,则∠AOC的度数是( )

A.75° B.90° C.105° D.125°
如图,等边ΔABC的边长为![]() cm,D、E分别是AB、AC上的点,将
cm,D、E分别是AB、AC上的点,将
ΔABC沿直线DE折叠,点A落在A′处,且A′在ΔABC外部,则阴影
部分图形的周长为( )cm.
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()

知正方形ABCD,E、F分别为边BC、CD上的点,DE=AF.
(1)求证:△ADF≌△DCE;
(2)求证:AF⊥DE.

x2+4x﹣1=0;
最近更新
- 在容积不变的密闭容器中,一定条件下发生反应:2AB(g)+2C(g),且达到平衡。当升高温度时气体的密度增大,则下列叙
- 如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是()A.6cm B.7
- 读图完成(1)-(4)小题。(10分)(1)图1中A、B两条河流,流程较长的是 ,流量较大的是 。(2分)
- .设,则的值为 .
- 安徽省太和县公安局曾因治安拘留争议被诉上法院,公安局长主动出庭,并要求全局中层以上干部旁听。从行政诉讼开始时的怕当被告、
- 在空间中,下列结论中正确的是 (A)垂直于同一平面的两个平面互相平行; (B)垂直于同一条直线的两条直线互相平行; (C
- 在消防知识中有一个词叫做“物理爆炸”,是指在没有发生化学反应的情况下发生的爆炸,下列各项描述中属于物理爆炸的是()
- Would you like spendyour holiday traveling by balloon? Now t
- 有人认为:“鸦片战争是在执行一种历史使命,它是用侵略手段来达到使中国向世界开放的目的,从某种意义上来说,是鸦片战争的一声
- The new high-speedrailway line between Urumqi, capital of th
- 依题后要求,在留空处填上适当的文字,使文意显豁、贯通。 (1)被人理解是幸运的,但不被人理解______________
- .函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图像如图所示,则f(0)的值是______
- 名著赏读(10分)【小题1】、请判断下列说法的正误,对的打“√”,错的打“×”。(4分)(1)“他的腿长步大,腰里非常的
- 下列说法正确的是() A.海南岛四面环海,水资源丰富,不必节约用水 B.明矾既能沉降水中的悬浮物,又能杀菌消毒 C.可通
- 下列描述分子结构的叙述中,正确的是() A. 6个碳原子都在一条直线上 B. 该烃属于苯的同系物
- 向盛有硫酸铜水溶液的试管里加入氨水,首先形成难溶物,继续添加氨水,难溶物溶解得到深蓝色的透明溶液。下列对此现象说法正确的
- D......
- 仿照划线部分,续写两个句子,使文段前后连贯。(4分)生命真是一个奇迹。一枝从污泥里长出来的夏荷,竟开出雪一样洁白纯净的花
- If you like, we _____ send you some samples(样品) of our late
- 观察下列顺序排列的等式:,….试猜想第个等式(为正整数): .



