初中 数学
化简 .
.
 .
.
下列运算正确的是( )
A . 7a3﹣3a2=4a
B . (a2)3=a5
C . a6÷a3=a2
D . ﹣a(﹣a+1)=a2﹣a
小敏将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°,感觉最舒适(如图1),侧面示意图为图2.使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O′C⊥OA于点C,O′C=12cm.

-
(1) 求∠CAO′的度数;
-
(2) 显示屏的顶部B′比原来升高了多少?
下列说法错误的是( )
A . 若  ,则
,则  B . 若定义运算“*”,规定
B . 若定义运算“*”,规定  则有
则有  C . 若
C . 若  ,则
,则  D . 若
D . 若  ,
,  ,则
,则 
 ,则
,则  B . 若定义运算“*”,规定
B . 若定义运算“*”,规定  则有
则有  C . 若
C . 若  ,则
,则  D . 若
D . 若  ,
,  ,则
,则 
已知点  ,
,  ,
,  都在反比例函数
都在反比例函数 
 的图像上,且
的图像上,且  ,则
,则  ,
,  ,
,  的大小关系是( )
的大小关系是( )
 ,
,  ,
,  都在反比例函数
都在反比例函数 
 的图像上,且
的图像上,且  ,则
,则  ,
,  ,
,  的大小关系是( )
的大小关系是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若一个正数的倒数是它本身,则这个数是。
已知方程  的解与方程
的解与方程  的解相同,则k的值是( )
的解相同,则k的值是( )
 的解与方程
的解与方程  的解相同,则k的值是( )
的解相同,则k的值是( )
A .  B .
B .  C . 2
D . -2
C . 2
D . -2
 B .
B .  C . 2
D . -2
C . 2
D . -2
下列算式中,运算结果为负数的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
单项式  的系数是,它的次数是.
的系数是,它的次数是.
 的系数是,它的次数是.
的系数是,它的次数是.
-
(1) 解不等式:
 并把解集表示在数轴上.
并把解集表示在数轴上. 
-
(2) 若关于x的不等式组
 的解为
的解为 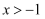 ,求a的值.
,求a的值.
疫情后为了复苏经济, 龙岗区举办了“春暖龙城,约惠龙岗”的促消费活动,该活动拿出1.1亿元,针对全区零售,餐饮,购车等领域出台优惠政策。为配合区的经济复苏政策,龙岗天虹超市同时推出了如下促销活动:
|
龙岗天虹超市促销活动方案: ①购物不足500元优惠15%(打8.5折) ②超过500元,其中500元优惠15%(打8.5折)超过部分优惠20%(打8折) |
-
(1) 小哲在促销活动时购买了原价为200元商品,他实际应支付多少元?
-
(2) 小哲在第一次购物后,在“龙岗发布”微信公众号中参与摇号抢到了一张满300减100的购物券(即微信支付300元以上自动减100元),又到龙岗天虹超市去购物,用微信实际支付了381元,他购买了原价多少元的商品?
已知y1=﹣x+3,y2=2x﹣3.
-
(1) 当x取何值时,y1=y2;
-
(2) 当x取何值时,y1的值比y2的值的2倍大8.
分数  介于两个相邻的整数之间,这两个整数是( )
介于两个相邻的整数之间,这两个整数是( )
 介于两个相邻的整数之间,这两个整数是( )
介于两个相邻的整数之间,这两个整数是( )
A . 3和4
B . 4和5
C . 5和6
D . 6和7
已知 , 则
, 则 .
.
 , 则
, 则 .
.
如图,在矩形  中,
中,  为边
为边  上一点,将
上一点,将  沿直线
沿直线  翻折,使得点
翻折,使得点  的对应点
的对应点  落在
落在  边上.若
边上.若  ,则
,则 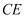 的长度是( )
的长度是( )
 中,
中,  为边
为边  上一点,将
上一点,将  沿直线
沿直线  翻折,使得点
翻折,使得点  的对应点
的对应点  落在
落在  边上.若
边上.若  ,则
,则 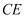 的长度是( )
的长度是( ) 
A .  B .
B .  C .
C .  D . 1
D . 1
 B .
B .  C .
C .  D . 1
D . 1
先化简,再求代数式  的值,其中
的值,其中  .
.
 的值,其中
的值,其中  .
.
如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.

-
(1) 判断△ABC的形状: ;
-
(2) 试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
-
(3)
当点P位于
 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
若|x﹣3|+(y+1)2=0,则x﹣2y的值为( )
A . 5
B . 0
C . 1
D . 2
一大门![]() 的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .

下列实数中,无理数是( )
A.-![]() B.π C.
B.π C.![]() D.|-2|
D.|-2|
最近更新
- 下列关于高等动物神经调节和体液调节的叙述,正确的是 A.寒冷环境中肾上腺素分泌量增加,将引起骨骼肌不自主战粟 B.刺激大
- 人们常引用孟子的“ , ”,强调建立
- 按照脂肪酸的分类,油酸应该属于哪一类脂肪酸? A.软脂肪酸 B花生四烯酸 C.硬脂肪酸 D.不饱和脂肪酸
- 物理知识在平时的生产生活中有广泛的应用,下列说法正确的是 A.电线的芯线外面包一层塑料,主要是为了保护里面的芯线
- 在根冠和衰老叶片中含量较多的植物激素是( ) A.脱落酸 B.乙烯 C.细胞分裂素
- 下表是二次函数的部分,的对应值: … 0123 ………(1)二次函数图象的开口向 ,顶点坐标是
- 下列应用的原理用化学方程式表示正确的是………………………………………( ) A.用电解水的方法测定水的组成
- that you are chosen to be a volunteer at the London
- —What about ______ grammar?--It'too boring.A.findingB.studyi
- Taste is such a subjective matter that we don’t usually cond
- 已知点在以原点为圆心的单位圆上运动,则点的轨迹是( ) A.圆 B.椭圆 C.双曲线
- 设方程x2–2x+m=0的两个根为a、b,且|a–b|=2,则实数m的值是 .
- 如图所示为画出的一条正弦曲线,横轴的单位是秒(s),下面说法正确的是( ) A.若纵轴的单位是米(m),这条曲线可
- 如图为氯化铵和硫酸钠的溶解度曲线,下列说法正确的是 A.将50℃时硫酸钠饱和溶液降温,始终有晶体析出 B.40℃时,将3
- —Jim! Is this your dictionary?—No, it isn't. Ask Sally. She
- 下列选项中哪些属于种群的特征( ) A.种群密度 B.物种丰富度 C.年龄组成
- 32.World leaders at the G20 summit conference in London deci
- 植物光合速率受多种环境因素的影响。下图表示在不同环境条件下某植物的光合速率变化情况,相关叙述正确的是 A.光照强度为1
- 材料一2008年3月,美国总统预选落下帷幕。希拉里在大选中获 胜。美国民主党战胜共和党夺得众议院和参议院的多数席位,从而
- 下列句子中没有语病且语义明确的一句是( )A.“千金易得,一将难求”,我们既要重视对引进人才的使用,也要切实提高原



