初中 数学
已知线段a、b满足2a=3b,则 =
=
 =
=
如图,⊙O是正五边形ABCDE的外接圆.若⊙O的半径为5,则半径OA , OB与 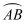 围成的扇形的面积是( )
围成的扇形的面积是( )
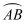 围成的扇形的面积是( )
围成的扇形的面积是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在正方形ABCD中,分别取AD、BC的中点E、F,并连接EF;以点F为圆心,FD的长为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则  的值为( )
的值为( )
 的值为( )
的值为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列数学符号中,既是轴对称图形,又是中心对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
有理数a,b在数轴上对应的位置如图所示,则下列选项正确的是( )
![]()
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
国家规定存款利息的纳税办法是:利息税=利息×5%;银行一年定期储蓄的年利率为2.25%,今年小刚取出一年到期的本金及利息时,交了4.5元的利息税,则小刚一年前存入银行的钱为( )
A . 2400元
B . 1800元
C . 4000元
D . 4400元
已知一组数据:5,15,75,45,25,75,45,35,45,35,那么40是这一组数据的( )
A . 平均数但不是中位数
B . 平均数也是中位数
C . 众数
D . 中位数但不是平均数
如图,一次函数y1=k1x+b与反比例函数  的图象相交于点A(1,﹣4)和点B(﹣2,m).
的图象相交于点A(1,﹣4)和点B(﹣2,m).
 的图象相交于点A(1,﹣4)和点B(﹣2,m).
的图象相交于点A(1,﹣4)和点B(﹣2,m).

-
(1) 分别求这两个函数的表达式;
-
(2) 连接AO,BO.求△AOB的面积;
-
(3) 若y2>y1>0,请直接写出满足条件的自变最x的取值范围.
两件商品都卖  元,其中一件亏本
元,其中一件亏本 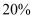 ,另一件盈利
,另一件盈利 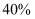 ,则两件商品卖出后总共盈利还是亏损?为什么?
,则两件商品卖出后总共盈利还是亏损?为什么?
 元,其中一件亏本
元,其中一件亏本 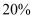 ,另一件盈利
,另一件盈利 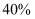 ,则两件商品卖出后总共盈利还是亏损?为什么?
,则两件商品卖出后总共盈利还是亏损?为什么?
如图,某公司组织员工假期去旅游,租用了一辆耗油量为每百公里约为25L的大巴车,大巴车出发前油箱有油100L,大巴车的平均速度为80km/h,行驶若干小时后,由于害怕油箱中的油不够,在途中加了一次油,油箱中剩余油量y(L)与行驶时间x(h)之间的关系如图所示,请根据图象回答下列问题:

-
(1) 汽车行驶 h后加油,中途加油 L;
-
(2) 求加油前油箱剩余油量y与行驶时间x的函数解析式;
-
(3) 若当油箱中剩余油量为10L时,油量表报警,提示需要加油,大巴车不再继续行驶,则该车最远能跑多远?此时,大巴车从出发到现在已经跑了多长时间?
若  ,
,  ,则
,则  =( )
=( )
 ,
,  ,则
,则  =( )
=( )
A .  B .
B .  C .
C . 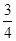 D .
D . 
若代数式  ,那么代数式
,那么代数式  的值是( )
的值是( )
 ,那么代数式
,那么代数式  的值是( )
的值是( )
A . -8
B . 16
C . 1
D . 6
如果关于x的不等式 (a+2016)x>a+2016的解集为x <1,那么a的取值范围是( )
A . a>-2016
B . a <-2016
C . a>2016
D . a<2016
某小区居民王先生改进用水设施,在5年内帮助他居住小区的居民累计节水39400吨,将39400用科学记数法表示应为.
已知:  的立方根是
的立方根是 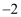 ,
,  的算术平方根3,
的算术平方根3,  是
是  的整数部分.
的整数部分.
 的立方根是
的立方根是 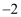 ,
,  的算术平方根3,
的算术平方根3,  是
是  的整数部分.
的整数部分.
-
(1) 求
 的值;
的值;
-
(2) 求
 的平方根.
的平方根.
已知M(1)=﹣2,M(2)=(﹣2)×(﹣2),M(3)=(﹣2)×(﹣2)×(﹣2),…,  .
.
 .
.
-
(1) 计算:M(5)+M(6)
-
(2) 求2M(2016)+M(2017)的值.
-
(3) 猜想2M(n)与M(n+1)的关系并说明理由.
在平面直角坐标系中,点  关于原点对称的点的坐标是.
关于原点对称的点的坐标是.
 关于原点对称的点的坐标是.
关于原点对称的点的坐标是.
用适当的方法解方程.
-
(1) 2x2﹣6x+1=0;
-
(2) 9(x﹣2)2=4 (2x+5)2 .
求 值:
![]()
如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
 |
最近更新
- 我国使用“长征3号甲”运载火箭的动力是由高氯酸铵(NH4ClO4)分解所提供的,反应方程式为2 NH4ClO4N2↑+C
- 先化简,再求值:2(2a2﹣5a)﹣4 (a2+3a﹣5),其中a=﹣2.
- 某强酸性溶液中含有大量Fe 2+ 、Fe 3+ 、Mg 2+ 和NH ,在该溶液中可以大量存在的阴离子是A . SOB
- 把一张透明塑料纸铺在桌面上,用筷子在塑料纸滴一个小水珠(直径约5mm),双手平拿着塑料纸,透过水珠看纸上的字比旁边的字_
- 如图所示,A、B是两只相同的齿轮,A被固定不能转动.若B齿轮绕A齿轮运动半周,到达图中C的位置,则此时B齿轮上标出的箭头
- 关于晶体的下列说法正确的是 …………( ) A.在晶体中只要有阴离子就一定有阳离子 B.在晶体中只要有阳离子就一定
- 推理是化学学习中常用的思维方法。下列推理正确的是( ) A.氧化物中都含有氧元素,所以含氧元素的化合物一定是氧化
- 电磁炮是一种理想的兵器,它的主要原理如图所示,利用这种装置可以把质量为2.0 g的弹体(包括金属杆EF的质量)加速到6
- 阅读下面一段文言文,完成问题。 王绂,字孟端,无锡人。博学,工歌诗,能书,写山木竹石,妙绝一时。洪武中,坐累戍朔州。永乐
- 下列各组离子一定能大量共存的是( ) A.在强碱溶液中:Na+、K+、AlO2-、CO32- B.在含大量Fe3+的溶
- (1)化合物A(C4H10O)是一种有机溶剂。A可以发生以下变化: ①A分子中的官能团名称是____
- 2.下列各句中,没有语病的一句是(2分) A.这家公司的利润近三个季度来一直下滑,根本原因是公司经营理念落后,产品质量下
- 设一元二次方程ax2+bx+c=0 (a≠0)的两根为m,n,则有如下关系: , ,根据以上关系填空:已知,x1,x2
- 下图所示的四种化合物的化学组成中, “O”所对应的名称相同的是 A.①② B. ①③ C. ②
- They did not find _____ to prepare for the worst conditions
- 读等高线图,回答下列问题: (1)D在E的______方;F点位于______地形部位上,其海拔高度是_____米。(2
- 下列物质在空气或氧气中燃烧时,现象描述正确的是 ( ) A. 红磷在
- – I’d like a pet, but I am busy all day. – Goldfish are a
- 假如英语课上老师要求同桌之间交换修改作文,请你修改你同桌的以下作文。文中共有10处错误,每句中最多有两处。错误涉及单词的
- 已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.(1)若点P到点A、点B的距离相等,求点



