初中 数学
计算
-
(1)

-
(2)

-
(3)

-
(4)

小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为.
一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )
A . 1.5
B . 2
C . 2.5
D . 3
如图,在梯形  中,
中,  是对角线
是对角线  的中点,联结
的中点,联结 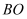 并延长交边
并延长交边  或边
或边  于E.
于E.
 中,
中,  是对角线
是对角线  的中点,联结
的中点,联结 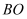 并延长交边
并延长交边  或边
或边  于E.
于E.

-
(1) 当点E在边
 上时,
上时,
①求证:
 ;
;②若
 ,求
,求  的值;
的值; -
(2) 若
 ,求
,求  的长.
的长.
若关于x的方程  的解是x=2,则a的值是( )
的解是x=2,则a的值是( )
 的解是x=2,则a的值是( )
的解是x=2,则a的值是( )
A . 6
B . -6
C . 4
D . 4
已知整数a.使得关于x的分式方程  +3=
+3=  有整数解.且关于x的一次函数y=(a﹣1)x+6﹣a的图象不经过第四象限,则所有满足条件的整数a的值的和是( )
有整数解.且关于x的一次函数y=(a﹣1)x+6﹣a的图象不经过第四象限,则所有满足条件的整数a的值的和是( )
 +3=
+3=  有整数解.且关于x的一次函数y=(a﹣1)x+6﹣a的图象不经过第四象限,则所有满足条件的整数a的值的和是( )
有整数解.且关于x的一次函数y=(a﹣1)x+6﹣a的图象不经过第四象限,则所有满足条件的整数a的值的和是( )
A . 10
B . 14
C . 16
D . 24
我国是一个干旱缺水严重的国家  我国的淡水资源总量为28000亿立方米,占全球水资源的
我国的淡水资源总量为28000亿立方米,占全球水资源的  ,仅次于巴西、俄罗斯和加拿大
,仅次于巴西、俄罗斯和加拿大  用科学记数法表示28000亿是
用科学记数法表示28000亿是 

 我国的淡水资源总量为28000亿立方米,占全球水资源的
我国的淡水资源总量为28000亿立方米,占全球水资源的  ,仅次于巴西、俄罗斯和加拿大
,仅次于巴西、俄罗斯和加拿大  用科学记数法表示28000亿是
用科学记数法表示28000亿是 

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若计算  的结果为正整数,则无理数m的值可以是.(写出一个符合条件的即可)
的结果为正整数,则无理数m的值可以是.(写出一个符合条件的即可)
 的结果为正整数,则无理数m的值可以是.(写出一个符合条件的即可)
的结果为正整数,则无理数m的值可以是.(写出一个符合条件的即可)
如图,分别延长▱ABCD的边AB、CD至点E、点F,连接CE、AF,其中∠E=∠F.求证:四边形AECF为平行四边形.

如图,把矩形纸片ABCD沿直线AE折叠,使点D落在BC边上的点F处,已知AB=6,BC=10,则线段CE的长为.

某校学生家庭作业完成时间情况的统计图如图所示,若该校作业完成时间在1小时内的学生有300人,则该校作业完成时间在2﹣3小时的学生有( )

A . 200人
B . 400人
C . 450人
D . 550人
某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
|
等级 |
A |
B |
C |
D |
|
频数 |
40 |
20 |
20 |
20 |
乙分厂产品等级的频数分布表
|
等级 |
A |
B |
C |
D |
|
频数 |
28 |
17 |
34 |
21 |
-
(1) 分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
-
(2) 分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
计算:  .
.
 .
.
如图,已知OA⊥OC,OB⊥OD,∠3=24°,求:∠1、∠2的度数.

已知二次函数y=ax2+bx+c的图象如图,下列结论:①abc>0;②b=2a;③a+b+c<0;④a-b+c>0.其中正确的个数是( )
A . 4个
B . 3个
C . 2个
D . 1个
某食品包装袋上标有“净含量385克±5克”,这包食品的合格净含量最大为.
如图,一束平行太阳光照射到正五边形上,若∠1=46°,则∠2= .

如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为( )

A . 50°
B . 60°
C . 70°
D . 80°
计算:  .
.
 .
.
式子﹣5﹣(﹣3)+(+6)﹣(﹣2)写成和的形式是( )
A. ﹣5+(+3)+(+6)+(﹣2) B.﹣5+(﹣3)+(+6)+(+2)
C. (﹣5)+(+3)+(+6)+(+2) D.(﹣5)+(+3)+(﹣6)+(+2)
最近更新
- 植物体的茎内,运输水分和无机盐的管道是;运输的管道是,二者属于组织.
- 作文。(60分)苏格拉底的学生曾向他请教人生的真谛,他把学生们领到一个果园说:“你们各自顺着一行果树从这头走到那头,每人
- (本小题满分12分) 如图,甲船以每小时海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于处时,乙船位于甲船
- 生物兴趣小组的同学设计了如图所示的实验装置,量筒内盛放的是澄清的石灰水,当向锥形瓶中注入清水后,量筒中澄清的石灰水变浑浊
- .印度地形自北向南依次是 A.山地、髙原、平原 B.山地、平原;髙原C.平原、髙原、山地 D.髙原、山地、平
- 近年来,召开听证会,邀请社会各界代表参与听证,认真听取大家的意见和建议,已成为我国各级政府部门进行决策的自觉行为。这一过
- 工业上大量获取乙烯的方法是: A.煤的气化 B.石油分馏 C.石油裂化 D.石油裂
- 下列说法正确的是()A. 22.4L任何气体的物质的量均为1mol B. 非标准状况下,1mol任何气体不可能占有22.
- 妈妈给小明买笔记本和圆珠笔.已知每本笔记本4元,每支圆珠笔3元,妈妈买了m本笔记本,n支圆珠笔.妈妈共花费 元.
- 一台“220V,60W”的电扇,一只“220V,60W”的白炽灯,一只“220V,60W”的电热器,将它们同时接在220
- 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.若AB=3,DE=2,BC=6
- 反应PCl5(g)PCl 3(g)+Cl2(g) ① 2HI(g) H2(g)+I2(g)
- 快递员通知小张中午12点到小区门口取快递,由于工作原因,快递员于11:50到12:10之间随机到达小区门口,并停留等待1
- 欣赏下面一首现代诗,回答问题(4分) 许 诺 汪国真不要太相信许诺许诺是时间结出的松果松果尽管美妙谁能保证不会被季节打落
- 我国三峡工程所提供的清洁、廉价、强劲、可再生的水电,相当于每年燃烧3×106t原煤的火力发电厂产生的电能。因此,三峡工程
- 仿照下面的示例,另写一句话。要求:句式基本一致,修辞相同。 示例:母爱如同疲惫时的一杯清茶,当你软弱无力时,淡雅
- 在下列各组溶液中,离子一定能大量共存的是 A.加入KSCN溶液显红色的溶液:K+、NH4+、Cl-、I- B.常温下,p
- 如图是食物经过人体消化道时,糖类.蛋白质和脂肪被化学消化的程度,字母表示组成消化道各器官的排列顺序.请据图回答.(1)曲
- 美国联邦制下,各州的权力主要是() A.处理本州范围内的事务 B.发行货币 C.对外宣战 D.对外缔结各种条约
- 国家干预主义主张通过财政政策和货币政策干预经济,扩张性财政政策对经济的影响是( ) A.缓和了经济萧条,但增加了政



