初中 数学
如图1,□ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.

-
(1) 求证:四边形 ABCD 是菱形;
-
(2) 若∠ADC=60°,BE=2,求BD的长.
如图,在 中,∠ACB=90°,AC=BC.点D是BC延长线上一点,连接AD.将线段AD绕点A逆时针旋转90°,得到线段AE.过点E作
中,∠ACB=90°,AC=BC.点D是BC延长线上一点,连接AD.将线段AD绕点A逆时针旋转90°,得到线段AE.过点E作 , 交AB于点F.
, 交AB于点F.
 中,∠ACB=90°,AC=BC.点D是BC延长线上一点,连接AD.将线段AD绕点A逆时针旋转90°,得到线段AE.过点E作
中,∠ACB=90°,AC=BC.点D是BC延长线上一点,连接AD.将线段AD绕点A逆时针旋转90°,得到线段AE.过点E作 , 交AB于点F.
, 交AB于点F.
-
(1) ①直接写出∠AFE的度数是 ▲ ;
②求证:∠DAC=∠E;
-
(2) 用等式表示线段AF与DC的数量关系,并证明.
如果等腰三角形的一个角是80°,那么它的底角是( ).
A . 80°或50°
B . 50°或20°
C . 80°或20°
D . 50°
如图,AC是半圆O的一条弦,以弦AC为折线将弧AC折叠后过圆心O,⊙O的半径为2,则圆中阴影部分的面积为.

计算:
-
(1)
 ;
;
-
(2)
 ;
;
-
(3)
 ;
;
-
(4)
 .
.
甲、乙两名篮球运动员进行每组10次的投篮训练,5组投篮结束后,两人的平均命中数都是7次,方差分别是 ,
,  , 则在本次训练中,运动员的成绩更稳定.
, 则在本次训练中,运动员的成绩更稳定.
 ,
,  , 则在本次训练中,运动员的成绩更稳定.
, 则在本次训练中,运动员的成绩更稳定.
如图,已知点A是反比例函数y=  (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
 (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( ) 
A . y=﹣  B . y=
B . y=  C . y=﹣
C . y=﹣  D . y=
D . y= 
 B . y=
B . y=  C . y=﹣
C . y=﹣  D . y=
D . y= 
已知平面直角坐标系中有一点 .
.
 .
.
-
(1) 若点M在x轴上,请求出点M的坐标.
-
(2) 若点
 , 且
, 且 轴,请求出点M的坐标.
轴,请求出点M的坐标.
已知  ABN和
ABN和  ACM位置如图所示,AB=AC,AD=AE,∠1=∠2,
ACM位置如图所示,AB=AC,AD=AE,∠1=∠2,
 ABN和
ABN和  ACM位置如图所示,AB=AC,AD=AE,∠1=∠2,
ACM位置如图所示,AB=AC,AD=AE,∠1=∠2, 
-
(1) 证明:BD=CE;
-
(2) 若∠M=40°,求∠N的度数.
下列图形中,既是中心对称图形又是轴对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
△ABC中,∠A=50°,∠B=60°,则∠C=度.
下面四个图形中,∠l与∠2是对顶角的图形是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  D .
D .
如图,已知  ,
,  .
.
 ,
,  .
. 
-
(1) 求证:
 是等边三角形;
是等边三角形;
-
(2) 求
 的度数.
的度数.
如图, ,
,  ,
,  , 则
, 则 的度数是( )
的度数是( )
 ,
,  ,
,  , 则
, 则 的度数是( )
的度数是( )
A . 30°
B . 40°
C . 50°
D . 60°
已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点.已知OE= 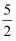 ,EF=3,求菱形ABCD的周长和面积.
,EF=3,求菱形ABCD的周长和面积.
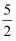 ,EF=3,求菱形ABCD的周长和面积.
,EF=3,求菱形ABCD的周长和面积. 
如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(  取1.73,结果保留整数)
取1.73,结果保留整数)
 取1.73,结果保留整数)
取1.73,结果保留整数)

下列事件中,确定事件是( )
A . 打开电视机,正在播放广告
B . 买一张电影票,座位号是奇数号
C . 3天内会下雨
D . 13个人中至少有2人生日在同一个月
在实数﹣  、0、﹣
、0、﹣  、2015、π、﹣
、2015、π、﹣ 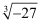 、0.1
、0.1  中,无理数的个数是( )
中,无理数的个数是( )
 、0、﹣
、0、﹣  、2015、π、﹣
、2015、π、﹣ 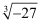 、0.1
、0.1  中,无理数的个数是( )
中,无理数的个数是( )
A . 2个
B . 3个
C . 4个
D . 5个
把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2017=( )
A . (31,51)
B . (32,48)
C . (33,47)
D . (34,43)
如图,以 
且
,则


,则
三者之间的关系为 ___________ .

最近更新
- 如图,Rt△ABC,∠ACB=90°,点D、E、F分别是三边的中点,且CF=5cm,则DE=___。
- 下列物质中既属于有机物,又属于酸的是 A.H2CO3 B.CH3OH C.CH3CH2OH D.CH
- ,出则无敌国外患者,国恒亡 。(《孟子》二章)
- 2008年,我ww w.ks 5u.c om国股票市场A股市值蒸发了22万亿元;每个账户平均损失38万元,很多股民体验了
- 下列说法中,错误的是A.有了化学科学,人类能够更好利用能源和资源 B.化学科学将为环境问题的解决
- The rich only ____ themselves in making money and had no eye
- 古诗文填空。(5题限选4题)(8分) 20. ,三岁食贫。淇水汤汤, 。(《诗经》) 21.丛菊
- 克罗地亚共和国是位于欧洲东南部的共和国,于2013年7月1日成为欧洲联盟第28个成员国。从此,克罗地亚人民() A.必须
- 剪去易拉罐的上部,并在上面蒙上半透明纸,在罐底部开一个小孔,用它做小孔成像实验,观察物体,下列说法中错误的是 (
- 依次填入下面一段文字横线处的语句,与上下文衔接最恰当的一组是( ) 岁月逶迤而来,蜿蜓远去, ________ 。我
- 如果你生活在19世纪后半期的欧洲,可能经历的事情有 ①拍卖行高价拍出梵·高的作品《向日葵》 ②
- 已知:①A从石油中获得是目前工业上生产的主要途径,A的产量通常用来衡量一个国家的石油化工发展水平;②2CH3CHO+O2
- 如图,在中,分别是边的中点,且,,则等于( )A. B. C. D.
- 药皂具有杀菌、消毒作用,制作药皂通常是在普通肥皂中加入了少量的 A.甲醛 B.酒精 C.苯酚
- 20.阅读下面四句话,找出加线词意义与其他三项不同的一项,并简要说明理由。(4分) ①杰富瑞,一条来自大洋彼岸的鲇鱼,在
- 石油之所以成为商品,是因为( ) A、石油是一种重要的战略物资 B、出现了作为流通手段的货币 C、使用价值和价值
- Short and shy, Ben Saunders was the last kid in his class
- 青蛙从幼体到成体,不可能出现的变化是 A. 鳃消失 B. 长出四肢 C. 尾消失 D.体表出现鳞片
- 下列各组离子能在呈酸性的无色溶滚中大量共存的是( ) A.Ba2+、Na+、NO3-、SO42- B.Mg
- 下图是“我国西气东输二线工程管线走向示意图”,读图完成下面小题。1.我国决定建设西气东输二线工程所考虑的最主要因素是 A



