初中 数学
将数据83,85,87,89,84,85,86,88,87,90分组,则 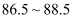 这一组的频数是.
这一组的频数是.
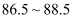 这一组的频数是.
这一组的频数是.
我军侦察员在距敌方120m的地方发现敌方的一座建筑物,但不知其高度又不能靠近建筑物物测量,机灵的侦察员将自己的食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住,如图所示.若此时眼睛到食指的距离约为40cm,食指的长约为8cm,则敌方建筑物的高度约是m.

如图,长方体的长为15,宽为10,高为20,点B与点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是。

这是某单位的平面示意图,已知大门的坐标为(﹣3,0),花坛的坐标为(0,﹣1).

⑴根据上述条件建立平面直角坐标系.
⑵建筑物A的坐标为(3,1),请在图中标出A点的位置.
如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是 (限填序号).

如图,在平面直角坐标系中,A(1, 2),B(3,
1),C(-2,
-1).

-
(1) 在图中作出
 关于
关于  轴对称的
轴对称的 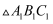 .
.
-
(2) 写出点
 的坐标(直接写答案).
的坐标(直接写答案). A1 , B1 ,C1 ;
-
(3) 求△ABC的面积.
已知4(x﹣1)2=25,则x=.
你认为下列各式正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,△OAB是等边三角形,点B在x轴的正半轴上,点A在反比例函数y=  (x>0)的图象上,则△OAB的面积为 。
(x>0)的图象上,则△OAB的面积为 。
 (x>0)的图象上,则△OAB的面积为 。
(x>0)的图象上,则△OAB的面积为 。

如图,在平行四边形ABCD中,∠A=40°,则∠C大小为( )

A . 40°
B . 80°
C . 140°
D . 180°
观察一组数据:2,4,7,11,16,22,29,  ,它们有一定的规律,记第一个数为
,它们有一定的规律,记第一个数为  ,第二个数记为
,第二个数记为  ,
,  ,第n个数记为
,第n个数记为  .
.
 ,它们有一定的规律,记第一个数为
,它们有一定的规律,记第一个数为  ,第二个数记为
,第二个数记为  ,
,  ,第n个数记为
,第n个数记为  .
.
-
(1) 请写出29后面的第一个数;
-
(2) 通过计算
 ,
,  ,
,  ,
,  由此推算
由此推算  的值;
的值;
-
(3) 根据你发现的规律求
 的值.
的值.
2019年年末,疫情影响了人们的正常出行,口罩一度成为热点。小红花可以到两家不同的医药超市购买口罩,两家医药超市的标价都是每包20元,但是甲药店规定一次购买5包以上,从第六包开始按照标价的80%卖。乙药店的优惠条件是每包都按照标价的85%卖。
-
(1) 写出甲药店中,总价y甲与购买包数x(包)(x>6)的关系式
-
(2) 若小红一次购买10包,去哪家购买划算?
已知一组数据x1 , x2 , x3 , x4的方差是2,则数据x1+5,x2+5,x3+5,x4+5的方差是.
化简:
-
(1)
 ;
;
-
(2)
 .
.
已知点A(a,1)与点B(5,b)关于原点对称,则ab的值为.
若等腰△ABC内接于⊙O,AB=AC,∠BOC=100°,则△ABC底角的度数为( )
A . 65°
B . 25°
C . 65°或25°
D . 65°或30°
如图,  是
是  的半径,过点M作
的半径,过点M作  的切线
的切线  ,且
,且  ,
,  ,
,  分别交
分别交  于点C,D,求证:
于点C,D,求证: 
 是
是  的半径,过点M作
的半径,过点M作  的切线
的切线  ,且
,且  ,
,  ,
,  分别交
分别交  于点C,D,求证:
于点C,D,求证: 

在数轴上,把表示数1的点称为基准点,记作点 . 对于两个不同的点M和N,若点M、点N到点
. 对于两个不同的点M和N,若点M、点N到点 的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点
的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
 . 对于两个不同的点M和N,若点M、点N到点
. 对于两个不同的点M和N,若点M、点N到点 的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点
的距离相等,则称点M与点N互为基准变换点.例如:图1中,点M表示数-1,点N表示数3,它们与基准点 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.
-
(1) 已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b=;若a=4,则b=;
②用含a的式子表示b,则b=;
-
(2) 对点A进行如下操作:先把点A表示的数乘以2.5,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是;
-
(3) 点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到
 ,
,  为
为 的基准变换点,点
的基准变换点,点 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到 ,
,  为
为 的基准变换点,…,依此顺序不断地重复,得到
的基准变换点,…,依此顺序不断地重复,得到 ,
,  , …,
, …, .
.  为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后 的落点为
的落点为 ,
,  为
为 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后 的落点为
的落点为 , …,依此顺序不断地重复,得到
, …,依此顺序不断地重复,得到 ,
,  , …,
, …, . 若无论k为何值,
. 若无论k为何值, 与
与 两点间的距离都是4,则n=
两点间的距离都是4,则n=
阅读下面材料,再回答问题:
有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是 。
(2)三角形的“二分线”可以是 。
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.

如图,AC是平行四边形ABCD的对角线,∠BCD=∠DAC.
(1)求证:AB=BC.
(2)若AB=2,AC=2![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.

最近更新
- 把代数式3x3-6x2y+3xy2因式分解,结果正确的是() A.x(3x+y)(x-3y) B.3x(
- 把a、b、c、d四块金属片浸入稀硫酸中,用导线两两相连组成原电池。若a、b相连时,a为负极;c、d相连时,电流由d到c;
- ......
- 生物学家发现一种病毒的长度约为0.00004349mm,保留两个有效数字并用科学记数法表示为________
- 已知曲线. (1)求曲线在点处的切线方程;(2)求曲线过点的切线方程.
- 用新鲜的紫色洋葱鳞片叶的内表皮为材料制成装片,经过下列试剂处理后置于显微镜下直接观察,有关说法正确的是 A.滴加30%蔗
- 现有下列实验装置图,结合该图回答下列问题:(1)写出图中标号仪器的名称:① ;②
- 根据中文、英文解释或句意填空1. My father is a very good ____________(游泳者).
- 阅读下面的文字,完成小题。 天职 许行 海尔曼博士的诊所远近闻名,在布拉沙市没有不知道他和他的诊所的。这个倔老头子,像他
- 化学与生产、生活、社会密切相关,下列有关说法不正确的是 A.“地沟油”可以制成肥皂,提高资源的利用率 B.为防止食品氧
- Carmen knew Mr Smith_______ gave a talk several months ago.A
- 有下列物质:①洁净的空气,②液氧,③水银,④冰水共存物 ⑤碘酒,⑥高锰酸钾,⑦二氧化碳 钾制氧气后的固体剩余物,⑧液态的
- 如图小华乘坐的是火车甲,窗外看到的是火车乙,试根据图片判断下列说法正确的是:A.以地面为参照物,乙火车一定是运动的 B.
- 已知数列{an}是正数组成的等差数列,Sn是其前n项的和,并且a3=5,a4S2=28.(1)求数列{an}的通项公式;
- 如图,物体A叠放在物体B上,B置于光滑水平面上,A、B质量分别为mA~=6kg、mB=2kg,A、B之间的动摩擦因数la
- 前几年美国根据我国古代花木兰的故事改编动画片在我国掀起热播狂潮,获得了巨大的商业利益。这给我们的启示是:( )
- The Bakers arrived last night, if they'd only let us know ea
- 在细胞有丝分裂期开始时,如果它的染色体数为N,DNA含量为Q,则该细胞分裂后每个子细胞中的染色体数和DNA含量分别是 A
- 2013年9月29日,“中国(上海)自由贸易实验区”正式挂牌。上海自贸区在金融领域试点一系列重大改革,具体包括:一是人民
- 圆:和圆:只有一条公切线,若,,且,则的最小值为 .



