初中 数学
-10的相反数是()
A . 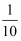 B . -
B . -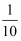 C . 10
D . -10
C . 10
D . -10
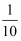 B . -
B . -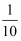 C . 10
D . -10
C . 10
D . -10
如图,在四边形ABCD中,  ,AC、BD相交于点E,若
,AC、BD相交于点E,若  ,则
,则  .
.
 ,AC、BD相交于点E,若
,AC、BD相交于点E,若  ,则
,则  .
. 
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.

阅读下列材料:小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为  ,求△ABC的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答:
,求△ABC的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答:
 ,求△ABC的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答:
,求△ABC的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答: 
-
(1) 图1中△ABC的面积为;
-
(2) 参考小明解决问题的方法,完成下列问题:
图2是一个6×6的正方形网格(每个小正方形的边长为1).
①利用构图法在答卷的图2中画出三边长分别为
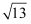 、2
、2  、
、  的格点△DEF;
的格点△DEF;②计算△DEF的面积.
如果点P(a,2)和点Q(﹣3,b)关于x轴对称,则点A(a,b)在第象限.
若  与
与  互为相反数,试求
互为相反数,试求 
 与
与  互为相反数,试求
互为相反数,试求 
下列各数:  ,
,  ,
,  ,1.414,
,1.414,  ,3.12122,
,3.12122,  ,3.161661666…(每两个1之间依次多1个6)中,无理数有个,有理数有个,负数有个,整数有个.
,3.161661666…(每两个1之间依次多1个6)中,无理数有个,有理数有个,负数有个,整数有个.
 ,
,  ,
,  ,1.414,
,1.414,  ,3.12122,
,3.12122,  ,3.161661666…(每两个1之间依次多1个6)中,无理数有个,有理数有个,负数有个,整数有个.
,3.161661666…(每两个1之间依次多1个6)中,无理数有个,有理数有个,负数有个,整数有个.
与方程x- =-1的解相同的方程是( )
=-1的解相同的方程是( )
 =-1的解相同的方程是( )
=-1的解相同的方程是( )
A . 3x-2x+2=-1
B . 3x-2x+3=-3
C . 2(x-5)=1
D .  x-3=0
x-3=0
 x-3=0
x-3=0
一个几何体的主视图、左视图、俯视图完全相同,它一定是( )
A . 圆柱
B . 圆锥
C . 球体
D . 长方体
一组数据3,4,5,5,6,8的极差是
A . 2
B . 3
C . 4
D . 5
如图,以边长为1的正方形ABCD的对角线AC为边,作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.若正方形ABCD的边长记为a1 , 按上述方法所作的正方形的边长依次记为a2、a3、a4、…、an , 则an=.

如图,在  中,A,B两个顶点在x轴的上方,顶点C的坐标是
中,A,B两个顶点在x轴的上方,顶点C的坐标是  .以点C为位似中心,在x轴的下方作
.以点C为位似中心,在x轴的下方作  的位似图形
的位似图形  ,并且
,并且  是把
是把  放大到原来的2倍后得到的.设点B的对应点
放大到原来的2倍后得到的.设点B的对应点 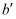 的横坐标是a,则点B的横坐标是.
的横坐标是a,则点B的横坐标是.
 中,A,B两个顶点在x轴的上方,顶点C的坐标是
中,A,B两个顶点在x轴的上方,顶点C的坐标是  .以点C为位似中心,在x轴的下方作
.以点C为位似中心,在x轴的下方作  的位似图形
的位似图形  ,并且
,并且  是把
是把  放大到原来的2倍后得到的.设点B的对应点
放大到原来的2倍后得到的.设点B的对应点 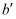 的横坐标是a,则点B的横坐标是.
的横坐标是a,则点B的横坐标是. 
若关于x的一元二次方程mx2+(m-1)x-10=0有一个根为x=2,则m的值是( )
A . -3
B . 2
C . -2
D . 3
在平面直角坐标系中,△ABC的三个顶点的位置如图所示,现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置.

-
(1) 在直角坐标系中,画出平移后所得△A′B′C′(其中B′、C′分别是B、C的对应点);
-
(2) 求△ABC的面积;
-
(3) 以A、B、C、D为顶点构造平行四边形,则D点坐标为.
计算:2cos30°+(π﹣4)0﹣ 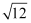 +|1﹣
+|1﹣  |+(
|+(  )﹣1 .
)﹣1 .
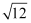 +|1﹣
+|1﹣  |+(
|+(  )﹣1 .
)﹣1 .
在数轴上表示a、b两个实数的点的位置如下图所示,则化简:│a-b│-│a+b│的结果为( )
![]()
A . 2a
B . 2b
C . 2a-2b
D . -2b
若y轴上的点A到x轴的距离为3,则点A的坐标为( )
A . (3,0)
B . (3,0)或(-3,0)
C . (0,3)
D . (0,3)或(0,-3)
不等式组 的解集为 .
的解集为 .
 的解集为 .
的解集为 .
据昌平交通局网上公布,地铁昌平线(一期)2015年1月4日出现上班运营高峰,各站进出站约47600人次. 将47 600用科学记数法表示为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
如图,已知∠1=∠2,∠3=∠4,EC=AD,求证:AB=BE

最近更新
- 中国第二届创业板高峰论坛于2010年10月31日在杭举行。本次峰会以“民企转型‘创’时代”为主题。创业板既是投资者的“升
- 中国古代几千年文明发展历程中,各民族的经济条件和社会制度存在着千差万别。现在中国,在一个多民族的国家中,只有承认这种差异
- 如图(a)所示,在以直角坐标系xOy的坐标原点O为圆心、半径为r的圆形区域内,存在磁感应强度大小为B、方向垂直xOy所
- F1、F2是双曲线=1的左、右焦点,P为该双曲线渐近线上一点,当PF1⊥PF2时,△PF1F2的面积为_________
- _______ can be good at something for40 years if he doesn’t
- (8分)1909年~1911年英国物理学家卢瑟福与其合作者做了用α粒子轰击金箔的实验.发现绝大多数α粒子穿过金箔后仍沿原
- 新疆绿洲的特色农产品主要有( )A.棉花、甜菜、瓜果 B.小麦、
- (本题满分10分) 解不等式或不等式组,并把它的解集在数轴上表示出来.
- I _____ sooner but I didn’t know that theywere waiting for
- 学习化学概念最主要的是弄清楚概念的实质和适用范围。电解质和非电解质的本质区别是什么?能否根据某物质的水溶液能导电来确定该
- 下图是东北地区地形剖面示意。读图回答问题。(1)从农业生产部门看,图中甲以 业为主,乙以
- 下列说法中,与“锲而不舍,金石可镂”包含同一哲理的是( ) ①近朱者赤,近墨者黑 ②城门失火,殃及池鱼 ③不积跬
- _____ their real economic situations, they got some relief f
- 用X代表F、Cl、Br、I四种卤族元素,下列属于它们共性的反应是( ) A.X2+H2O====HX+HXO
- 给出下列器材:A、电压为3V的电源; B、量程为3V的电压表;C、量程为15V的电压表; D、量程为
- 计算:(2﹣1)2﹣( +)(﹣).
- 下列操作能达到实验目的是()选项 实 验 目 的 实 验 操作 A 验证金属性Na大于铁 向FeCl3溶液中加金属钠,观
- 所以说十一届三中全会是建国以来党的历史上具有深远意义的历史转折,主要是因为A.恢复了的职务B.进行了真理标准问题的讨论C
- 公园里多种颜色的塔菊花是利用了什么方法做到的( ) A.种子繁殖 B.压条 C.嫁接
- 20世纪90年代,有人评论国际局势说:当今世界,巨人林立.日本是独脚巨人,俄罗斯是生病的巨人,欧洲是缺乏凝聚力的巨人,美



