初中 数学
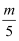 >
>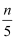 C . ﹣3m<﹣3n
D . 2m+1<2n+1
C . ﹣3m<﹣3n
D . 2m+1<2n+1




 ,则( )
,则( )
 =.
=.
 D . 一个正数一定大于它的倒数
D . 一个正数一定大于它的倒数
 与y轴交于点C , 顶点为D . 直线
与y轴交于点C , 顶点为D . 直线  交x轴于点E , 点F在直线
交x轴于点E , 点F在直线  上,且橫坐标为4,现在,将抛物线沿其对称轴上下平移,使抛物线与线段
上,且橫坐标为4,现在,将抛物线沿其对称轴上下平移,使抛物线与线段  总有公共点.抛物线向上最多可以平移个单位长度,向下最多可以平移个单位长度.
总有公共点.抛物线向上最多可以平移个单位长度,向下最多可以平移个单位长度.

 ,则
,则  =.
=.
 ,由于甲看错了方程①中的a,得到方程组的解为
,由于甲看错了方程①中的a,得到方程组的解为 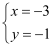 ,乙看错了方程②中的b,得到方程组的解为
,乙看错了方程②中的b,得到方程组的解为  ,试计算a2019+(﹣
,试计算a2019+(﹣ 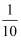 b)2018 .
b)2018 .
 .
.
 B .
B .  C .
C .  D .
D . 

 为( )
为( )
 B .
B .  C .
C .  D .
D . 
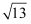 ﹣1的值在( )
﹣1的值在( )
一个正三角形至少绕其中心旋转_________,就能与其自身重合;一个正六边形至少绕其中心旋转_________,就能与其自身重合.
如图所示,一个圆柱体的高为6cm,底面半径为![]() cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是__________.
cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是__________.

如图,直线 
与









( 1 )写出列各点的坐标 

( 2 )求点 

( 3 )若点 




( 4 )若点 








的面积等于 4.5 ,并求出此时点

( 5 )若直线 





一次函数y=ax+c(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )


- (2009年安徽文综)下图为某地区港口分布示意图。回答3~4题。3.导致a港口解冻日期比其他港口晚的主要因素是 A.地形
- 阅读下面语段,回答问题: 文化程度高的人一般说来信息来源比较广、语言能力比较好、适应国外生活的能力比较强,所以容易迁移成
- 下面关于植物细胞工程的叙述,正确的是 A. 叶肉细胞脱分化后可形成薄壁细胞B.叶肉细胞经再分化过程可形成愈伤组织 C.
- 下图表示细胞内某些有机物的元素组成和功能关系,其中A、B代表元素,Ⅰ、Ⅱ、Ⅲ、Ⅳ是生物大分子,图中X、Y、Z、P分别为构
- 下列划线字注音完全正确的一项是( )(2分) A.和蔼(ǎi)颓唐(tuí)倜傥(tì dǎng)弥漫(mí) B.
- 一定温度下,在下图所示装置中,固体X与气体Y反应生成气态产物,当改变温度时该气态产物发生逆向反应,重新生成X和Y.发生的
- 在一位名叫PuzzledMom的学生家长的博客上,你看到了以下内容。请根据该博客,给这位家长回复,词数为120左右。 I
- 如图△中,∠=90°,=4,=5,点是上的一个动点(不与点、点重合),PQ⊥,垂足为Q,当PQ与△的内切圆⊙O相切时,的
- (6分)在一体积固定的密闭容器中加入反应物A、B,发生如下反应:A + 3B == 2C 。反应经2min后,A的浓度从
- 38.C1、C2、C3、C4是某动物的4个细胞,其染色体数分别是N、2N、2N、4N,下列相关叙述错误的是() A.C1
- 数列{an}是正数组成的等比数列,公比q=2,a1a2a3……a20=a50,,则a2a4a6……a20的值为 (
- 小明以水蕴草为材料进行了下图所示的实验,并定时记录试管顶端的气体量。该实验的主要目的是探究 ( )A.水量对呼吸作用速
- 思格斯称赞一位近代科学家的研究成就是“自然科学的独立宣言”,他指的应是 A.哥白尼的“日心说”否定了宗教神学崇信的“地心
- 将SO2气体通入BaCl2溶液至饱和,未见有沉淀生成,继续通入另一种气体仍无沉淀产生,则通入的气体可能是 A. N
- 漫画《无题》(作者:周喜悦)中主角的行为表明 ①实践是检验认识真理性的标准 ②规律具有客观性和普遍性 ③意识活动具有自觉
- 已知a=(1-t,1-t,t),b=(2,t,t),则|b-a|的最小值是( ) A.
- 2013年11月3日至5日,习书记在湖南考察时,同村干部和村民代表围坐在一起,亲切地拉家常、话发展。他表示,我这次到湘西
- 2013年12月28日,春运首日火车票全面开售,小王花了65元在12306网购了一张回家的火车票,65元在这里体现了货币
- 古代诗歌阅读(11 分) 送琴师毛敏仲北行 南宋·汪元量 西塞山前日落处,北关门外雨来天。 南人堕泪北人笑,臣甫低头拜杜
- 如图4-1-14所示,质量相等的物体A和物体B与地面的动摩擦因数相等,在恒力F的作用下,一起沿水平地面向右移动x,则



