初中数学：七年级　 八年级　 九年级　 中考　

初中数学

如图，△ABC的顶点坐标分别为A（0，3），B（2，1），C（2，-3），则△ABC的外心坐标是．

当x＝2时，代数式ax³＋bx＋4的值为8，那么当x＝－2时，这个代数式的值为．

如图，点E、F在BC上，BE=FC，AB=DC，∠B=∠C．求证：∠A=∠D．

如图，二次函数y₁=ax²+bx+3的图像与x轴相交于点A（﹣3，0）、B（1，0），交y轴于点C，C，D是二次函数图象上的一对对称点，一次函数y₂=mx+n的图像经过B、D两点．

（1）求二次函数的解析式及点D的坐标；
（2）根据图像写出y₂＞y₁时，x的取值范围．

如图，为估算某河的宽度，在河对岸选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上．若测得BE＝20m，EC＝10m，CD＝20m，则河的宽度AB＝m．

图片_x0020_134911610

某中学开学初到商场购买A.B两种品牌的足球，购买A种品牌的足球50个，B种品牌的足球25个，共花费4500元.已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元

（1）求购买一个A种品牌、一个B种品牌的足球各需多少元?
（2）学校为了响应习总书记“足球进校园”的号召，决定再次购进A.B两种品牌足球共50个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高4元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A.B两种品牌足球的总费用不超过第一次花费的70%，且保证这次购买的B种品牌足球不少于23个，则这次学校有哪几种购买方案?

如图所示，在□ABCD中，对角线AC与BD相交于点O ， M ， N在对角线AC上，且AM=CN ，则BM与DN的关系是（）.

A . BM∥DN B . BM∥DN,BM=DN C . BM=DN D . 没有关系

下列运算正确的是( )

A .

x•x³=x³

B . x²+x²=x⁴ C . （-4xy²）²=8x²y⁴ D . （-2x²)（-4x³)=8x⁵

如图，四边形 $\text{[math]}$ 的两条对角线 $\text{[math]}$ 所成的锐角为 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的面积最大值为．

如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的边长为（　　）

A . 9 B . 12 C . 15 D . 18

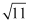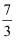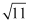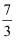下列实数中： $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、0.1010010001…（往后每两个1之间依次多一个0），无理数有（　　）

A . 2个 B . 3个 C . 4个 D . 5个

在一个不透明的袋子中装有3个除颜色外完全相同的小球，其中白球1个、黄球1个、红球1个，摸出一个球记下颜色后放回，再摸出一个球，记下相应颜色．

（1）请用列表法或画树状图法表示出两次所得颜色的所有可能情形；
（2）求两次摸到的球同色的概率．

如图，已知AB∥CD∥EF，直线AF与直线BE相交于点O，下列结论错误的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

2的相反数的倒数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . ﹣2

设“●”、“▲”表示两种不同的物体，现用天平称（如图），若用x、y分别表示“●”、“▲”的重量，写出正确的不等式是．

一个两位数，若个位数字为a，十位数字为b，则这个两位数可表示为．

若数轴经过折叠， $\text{[math]}$ 表示的点与 $\text{[math]}$ 表示的点重合，则 $\text{[math]}$ 表示的点与数表示的点重合．

如图是超市中某品牌的洗发水的价格标签，一服务员不小心将墨水滴在标签上，使得原价看不清楚，请

帮忙算一算，该洗发水的原价是元．

沙坪坝三峡广场原有一块长为米，宽为米的长方形地块，现在政府对广场进行改造，计划将如图四周阴影部分进行绿化，中间将保留边长为米的正方形雕像，则绿化的面积是多少平方米？并求出当时的绿化面积．

将圆柱形纸筒沿母线剪开铺平，得到一个矩形（如图）．如果将这个纸筒沿线路剪开铺平，得到的图形是（）

A．矩形 B．半圆 C．三角形 D．平行四边形

最近更新

　