初中 数学
如图,四边形ABCD是等腰梯形,∠ABC=60°,若其四边满足长度的众数为5,平均数为 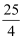 ,上、下底之比为1:2,则BD的长是( ).
,上、下底之比为1:2,则BD的长是( ).
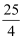 ,上、下底之比为1:2,则BD的长是( ).
,上、下底之比为1:2,则BD的长是( ).
A . 5
B . 5  C . 3
C . 3  D . 3
D . 3 
 D . 3
D . 3 
比较两个角 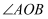 和
和 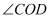 的大小关系:小明用度量法测得
的大小关系:小明用度量法测得  ;小丽采用叠合法比较这两个角的大小,她将
;小丽采用叠合法比较这两个角的大小,她将 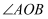 和
和 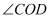 的顶点重合,边
的顶点重合,边  与
与  重合,边
重合,边  和
和 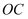 置于重合边的同侧,则边
置于重合边的同侧,则边  .(填序号:①“在
.(填序号:①“在 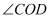 的内部”;②“在
的内部”;②“在 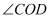 的外部”;③“与边
的外部”;③“与边 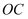 重合”)
重合”)
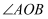 和
和 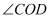 的大小关系:小明用度量法测得
的大小关系:小明用度量法测得  ;小丽采用叠合法比较这两个角的大小,她将
;小丽采用叠合法比较这两个角的大小,她将 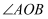 和
和 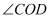 的顶点重合,边
的顶点重合,边  与
与  重合,边
重合,边  和
和 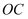 置于重合边的同侧,则边
置于重合边的同侧,则边  .(填序号:①“在
.(填序号:①“在 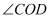 的内部”;②“在
的内部”;②“在 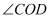 的外部”;③“与边
的外部”;③“与边 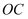 重合”)
重合”)
甲、乙两个工程队修筑一条公路,甲队从南向北方向修筑,乙队从北向南方向修筑.甲、乙两队同时开工,乙队施工几天后因另有任务提前离开,甲队继续修筑公路.当乙队任务完成后,因赶时间,乙队回来继续修筑公路,直到公路修通.在修路过程中,甲、乙两队的工作效率保持不变.设甲、乙两队修筑公路的长度为y(米),施工时间为x(天),y与x之间的函数图象如图所示.

-
(1) 甲队每天修筑公路米,乙队每天修筑公路米;
-
(2) 求乙队离开的天数;
-
(3) 求乙队回来后修筑公路的长度y与x之间的函数关系式,并写出自变量x的取值范围;
-
(4) 求这条公路的总长度.
下列命题中,正确命题是( )
A . 两个角是直角的四边形是直角梯形
B . 一组对边相等,另一组对边平行的四边形是平行四边形
C . 四个角都相等的四边形是正方形
D . 对角互补的梯形是等腰梯形
已知a,b均为实数,且a<b,下列不等式中一定成立的是( )
A . a-1>b-1
B . 3a<3b
C . -a<-b
D . a-2>b-2
已知有50个数据分别落在五个小组内,落在第一、二、三、五小组内的数据个数分别为2,8,15,15,则落在第四小组内的频率是.
不超过54的正整数中,奇数有个,偶数有个。
已知有理数 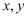 满足
满足  ,则
,则  .
.
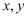 满足
满足  ,则
,则  .
.
求下列各式中x的值.
(1)4x2﹣ =0;
=0;
(2)(3x+2)3﹣1= .
.
计算:  .
.
 .
.
关于函数y=﹣2x+3,下列说法中不正确的是( )
A . 该函数是一次函数
B . 该函数的图象经过一、二、四象限
C . 当x值增大时,函数y值也增大
D . 当x=﹣1时,y=5
计算:|﹣4|+  ﹣
﹣  ﹣
﹣  cos45°.
cos45°.
 ﹣
﹣  ﹣
﹣  cos45°.
cos45°.
下面四个数中,无理数是( )
A . 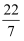 B .
B .  C .
C .  D . ﹣
D . ﹣ 
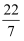 B .
B .  C .
C .  D . ﹣
D . ﹣ 
如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为.

求满足下列各式的未知数x的值.
-
(1)

-
(2)

世界文化遗产长城总长约670000米,将数670000用科学记数法可表示为( )
A . 6.7×104
B . 6.7×105
C . 6.7×106
D . 67×104
如图1,在等边△ABC中,点E从顶点A出发,沿AB的方向运动,同时,点D从顶点B出发,沿BC的方向运动,它们的速度相同,当点E到达点B时, D、E两点同时停止运动.
(1)求证:CE=AD;
(2)连接AD、CE交于点M,则在D、E运动的过程中,∠CMD变化吗?若变化,则说明理由;若不变,则求出它的度数;
(3)如图2,若点D从顶点B出发后,沿BC相反的方向运动,其它条件![]() 不变. 求证:CE=DE.
不变. 求证:CE=DE.

如图,⊙O过点B、C,圆心O在等腰Rt△ABC的内部,∠BAC=90°,OA=2,BC=8.则⊙O的半径为( )

A.![]() B.5 C.
B.5 C.![]() D.6
D.6
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C,若∠ACB=30°,AB=![]() ,则阴影部分的面积是 .
,则阴影部分的面积是 .

下列说法中,正确的是( )
A.3是单项式
B.﹣![]() 的系数是﹣3,次数是3
的系数是﹣3,次数是3
C.![]() 不是整式
不是整式
D.多项式2x2y﹣xy是五次二项式
最近更新
- 美国是典型的联邦制国家,下列关于联邦政府与州政府的关系说法正确的有() ①联邦与州分享政治权力 ②各州的权力是联邦政府授
- 奥斯特实验说明了( ) A.磁场的存在 B.磁场
- 设P为曲线C:y=x2-x+1上一点,曲线C在点P处的切线的斜率的范围是[-1,3],则点P纵坐标的取值范围是_____
- 下列实验操作、现象与所得结论一致的是实验操作 现象 结论 A 向盛有25mL沸水的烧杯中滴加5~6滴FeCl3饱和溶液,
- 已知函数f(2x+1)=3x+2,且f(a)=4,则a=________.
- 设是函数的极值点,数列满足表示不超过的最大整数,则 ___________.
- 文艺复兴和启蒙运动为近代欧洲的发展奠定了思想基础,其共同点有( ) A.反对宗教神学,强调自由、解放 B.
- 每年三月,春花烂漫时,我国都要召开全国人民代表大会和全国政治协商会议,全国人大代表和全国政协委员汇集北京,共商国是。人大
- 2010年1月11日,国家科学技术奖励大会在北京人民大会堂隆重举行。中国科学院院士谷超豪、孙家栋荣获2009年度国家最高
- 3.下列各句中,加点的词语运用正确的一项是( ) A.生活的心酸并没有击败李明对音乐的执着,他很感激老天能够给他
- 下列关于群落演替的叙述不正确的是( ) A.演替是群落的根本性质发生变化的现象 B.演替过程只要不遭到人类的破坏
- . —I have to get to the post office by six o’clock, but it i
- 某无色溶液能与镁反应放出氢气,此溶液中可能大量共存的离子组是A.H+, Ba2+, Mg2+, Cl-
- 在如图所示的食物网中,假如猫头鹰的食物有2/5来自于兔子,2/5来自于鼠,1/5来自于蛇,那么猫头鹰增加20g体重,最少
- 关于平抛运动,下列说法中正确的是 A.平抛物体在运动过程中,其加速度和水平速度保持不变 B.平抛运动
- 4的算术平方根是 .
- 如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB=60°,AC=16,则图中长度为8的线段有()
- 礼 物灯光很暗,女儿在母亲的床边站了一会儿,然后轻轻地把一个包装很精致的工艺品盒放在母亲的身边。那是女儿送给母亲的生日礼
- 家用的手电筒.用干电池作电源.正常发光时电流为O.32A.小灯泡的电功率接近: A.1W B.10W C.
- 细胞中既由双层膜组成,又能让某些大分子通过的膜是 ( ) A.线粒体膜 B



