初中 数学
如图,用四个螺丝将四条不可弯曲的木条围成一个木框,水条长度分别为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条使木框成为一个三角形,则所有三角形中边最长为( )

A . 6
B . 7
C . 8
D . 10
已知直角三角形两直角边a,b满足  ,则斜边c上中线的长为.
,则斜边c上中线的长为.
 ,则斜边c上中线的长为.
,则斜边c上中线的长为.
已知直线 , 动点C在
, 动点C在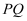 与
与 之间.
之间.
 , 动点C在
, 动点C在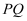 与
与 之间.
之间.

-
(1) 如图1,若
 与
与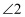 都是锐角,求
都是锐角,求 三者之间的数量关系;
三者之间的数量关系;
-
(2) 如图2,将一块三角尺(其中
 )按图中位置摆放,点D,E,F是三角尺的边与平行线的交点,若
)按图中位置摆放,点D,E,F是三角尺的边与平行线的交点,若 , 求
, 求 的度数;
的度数;
-
(3) 如图3,将图2中的三角尺进行适当转动,直角顶点C始终在两条平行线之间,点G在线段
 上,且
上,且 , 求
, 求 与
与 之间的数量关系.
之间的数量关系.
如图,两支温度计的读数分别是某一时刻小明家阳台与室内的气温,那么这一刻阳台的气温比室内气温低( )


A . 5℃
B . 12℃
C . 7℃
D . 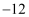 ℃
℃
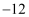 ℃
℃
从一堆苹果中任取了20个,称得它们的质量(单位:克),其数据分布表如下.则这堆苹果中,质量不小于120克的苹果数约占苹果总数的( )
分组 | (90,100) | (100,110) | (110,120) | (120,130) | (130,140) | (140,150) |
频数 | 1 | 2 | 3 | 10 | 3 | 1 |
A . 80%
B . 70%
C . 40%
D . 35%
已知⊙O的直径为10,圆心O到弦AB的距离OM为3,则弦AB的长是( )
A . 4
B . 6
C . 7
D . 8
函数y=  中自变量x的取值范围是( )
中自变量x的取值范围是( )
 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A . x≥0
B . x>2
C . x≠2
D . x≥2
已知A=xy﹣2y2+3x2 , B=xy﹣4y2 , C=2B﹣5A .
-
(1) 求C的表达式;
-
(2) 当x=﹣1,y
 ,求C的值.
,求C的值.
将矩形纸片OABC放在平面直角坐标系中,O为坐标原点,点A在y轴上,点C在x轴上,点B的坐标是(8,6),点P是边AB上的一个动点,将△OAP沿OP折叠,使点A落在点Q处.
-
(1) 如图①.当点Q恰好落在OB上时.求点P的坐标;

-
(2) 如图②,当点P是AB中点时,直线OQ交BC于M点;

(a)求证:MB=MQ;(b)求点Q的坐标.
计算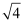 的结果是( )
的结果是( )
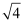 的结果是( )
的结果是( )
A . 2
B . ±2
C . -2
D . ±

若代数式4x+13的值不小于代数式2x﹣1的值,则x的取值范围是.
关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则实数k的取值范围是 .
将点  先向上平移
先向上平移  个单位,再向左平移
个单位,再向左平移  个单位,得到点
个单位,得到点  ,则点
,则点  的坐标为.
的坐标为.
 先向上平移
先向上平移  个单位,再向左平移
个单位,再向左平移  个单位,得到点
个单位,得到点  ,则点
,则点  的坐标为.
的坐标为.
若不等式组  无解,则有( )
无解,则有( )
 无解,则有( )
无解,则有( )
A . b>a
B . b<a
C . b=a
D . b≤a
已知  与
与  互为相反数,则
互为相反数,则 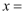
 与
与  互为相反数,则
互为相反数,则 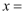
如图是4×4正方形网格,其中已有3个小方格涂成了阴影.现在要从其余13个白色小方格中选出一个也涂成阴影,使整个涂成阴影的图形成为轴对称图形,请在图中补全图形,并画出它们各自的对称轴.(要求画出3种不同方法)

先化简,后求值
![]() , 其中a= -
, 其中a= -![]() .
.
如图,在灯塔 处观测到轮船
位于北偏西

在南偏东

的大小为( )

A . B .



已知空气的单位体积质量为1.29×10﹣3克/厘米3,1.29×10﹣3用小数表示为( )
A.0.00129 B.0.0129 C.﹣0.00129 D.0.000129
已知关于x的一元二次方程(k-2)2x2+(2k+1)x+1=0有两个不相等的实数根,则k的取值范围是 ▲ .
最近更新
- 已知二元二次方程:,a∈R.给出以下说法: ① 无论a为何值,该方程均可表示半径不为0的圆; ② 无论a为何值,该方程所
- 1.下列各组句子中,加横线的词的意义和用法相同的一项是()(2分) A.①视为止,行为迟 ②为诸君溃围 B.
- 材料一:中国人民银行宣布,自2010年12月26日起金融机构一年期人民币存贷款基准利率分别上调0.25个百分点,这是20
- 下列物质在空气或氧气中燃烧时,现象描述正确的是 A.木炭在氧气中燃烧,发出白光,放出热量,产生二氧化碳气体
- 太平天国运动失败的根本原因是A .农民阶级的局限性B .拜上帝教不符合中国国情C .在军事策略上的失败D .中外反动势力
- 图2为某植株在夏季晴天一昼夜内CO2吸收速率的变化情况,以下判断正确的是( ) A.影响bc段光合速率的外界因素只
- 文庙是中国古代官方兴建的祭祀孔子的场所,产生于唐代,宋代逐渐在中原、江南的城市中大量兴建,元代在贵州、云南,清代在新疆、
- Food prices increased ________ 10% in less than a year.A. fo
- 阅读:如果把一个多项式分组并提取公因式后,各组之间又有公因式,那么这个多项式就可以用分组分解法来分解因式.请举例说明你对
- 在鱼塘中混合放养多种鱼可以提高产量,如图所示,下列叙述不正确的是
- 下列说法正确的是 【
- 1944年6月6日,美英盟军在诺曼底登陆,开辟了第二战场,请问:这个第二战场是相对于哪个战场来说的 A、北非战场
- 设直线l:x+2y+1=0交椭圆C:4(x-1)2+9(y+2)2=36于A、B两点,在椭圆上求一点P,使△ABP的面积
- 下列句子中加横线词语使用正确的一项是( ) A.小明经常到老人院做好事,他的事迹真是罄竹难书。 B.每个考生都应充分
- 在一定条件下,萘可以和硝酸、硫酸和混合酸发生硝化反应,生成二硝基物,它是1,5-二硝基萘和1,8—二硝基萘的混合物。后者
- 依次填入下面一段文字横线处的语句,衔接最恰当的一组是(3分) 九成宫,在陕西麟游县城西,本为隋开皇十三年至十五年建造的仁
- (16分)如图所示,在倾角为θ=37°的足够长的固定斜面上,物体A和小车B正沿着斜面上滑,A的质量为mA=0.50kg,
- 易中天在《艰难的一跃》中说,这部宪法的出现究竟是人性与自由的胜利,还是利益力量左右的结果?这是一个需要回答、却又不必认真
- 罗斯福说:“低收入的工人是我们人数最多的消费集团,可是今天他们却无法维持像样的生活水准,不能购买食品、衣服和其他必需品—
- 下表中实验操作能达到实验目的的是 ( )选项 实验操作 实验目的



