初中数学：七年级　 八年级　 九年级　 中考　

初中数学

等腰三角形的两边长分别是3和7,则其周长为（）

A . 13 B . 17 C . 14 D . 13或17

计算：

（1） (-2)²+(π- $\text{[math]}$ )⁰-（- $\text{[math]}$ ）^-2
（2）（2x-1）²-(x-1)(x+1)

已知关于x的一元二次方程 $\text{[math]}$ $\text{[math]}$ ．

（1）求证：此方程总有两个不相等的实数根；
（2）若此方程的两个根都为整数，求整数a的值．

如图，在⊙O中，AB为直径，AC=5，AB=10，

图片_x0020_100016

（1）作以AC为底边的圆内接等腰△ACD；（要求：尺规作图，不写作法，保留作图痕迹）
（2）求弦AC所对的圆周角。

对下列问题，有三位同学提出了各自的想法：

若方程组 $\text{[math]}$ 的解是 $\text{[math]}$ ，求方程组 $\text{[math]}$ 方程组的解．

甲说：“这个题目的好象条件不够，不能求解”；

乙说：“它们的系数有一定的规律，可以试试”；

丙说：“能不能把第二个方程组的两个方程的两边都除以4，通过换元的方法来解决”．

请根据他们的讨论，求出第二个方程组的解．

在平面直角坐标系中，点A(-3，2)关于x轴的对称点坐标为( )

A . (2，-3) B . (3，2) C . (3，-2) D . (-3，-2)

解分式方程：

（1） $\text{[math]}$
（2） $\text{[math]}$

计算： $\text{[math]}$ +（ $\text{[math]}$ ﹣1）⁰+（﹣1）²²=．

如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转，得到 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 的对应点分别是点E，D，点E在AB边上．

（1）若 $\text{[math]}$ 是 $\text{[math]}$ 的中点，则DB=；
（2）若 $\text{[math]}$ ，则点D到 $\text{[math]}$ 的距离为．

如图，⊙ $\text{[math]}$ 中，弦 $\text{[math]}$ 与 $\text{[math]}$ 相交于点E, $\text{[math]}$ ,连接 $\text{[math]}$ .

求证：

（1） $\text{[math]}$ ；
（2） $\text{[math]}$ .

如图，在矩形ABCD中，AC，BD相交于点O，根据矩形的性质，AO=OB=OC=0D= $\text{[math]}$ AC= $\text{[math]}$ BD，由此我们得到直角三角形的一个性质：直角三角形斜边上的中线等于斜边的．

（1）在矩形ABCD中，AB=1，BC=2，则对角线AC的长等于　　．

（2）在矩形ABCD中，AB=1，BC=2，则Rt△ABC中，斜边AC边上的中线等于　　．

如图，是由线段AB，CD，DF，BF，CA组成的平面图形，∠D=28°，则∠A+∠B+∠C+∠F的度数为．

已知反比例函数 $\text{[math]}$ ，下列说法不正确的是( )

A . 图形经过点(2，-4) B . 当x≤-8时，0<y≤1 C . y随x的增大而增大 D . 图象在二、四象限

在平面直角坐标系中，已知平行四边形ABCD的三个顶点坐标分别是A（m，n），B（2，-1），C（-m，-n），则关于点D的说法正确的是（）

甲：点D在第一象限

乙：点D与点A关于原点对称

丙：点D的坐标是（-2，1）

丁：点D与原点距离是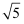 $\text{[math]}$ .

A . 甲乙 B . 乙丙 C . 甲丁 D . 丙丁

计算：＝ .

如图，四边形ABCD内接于⊙O，并且AD是⊙O的直径，C是弧BD的中点，AB和DC的延长线交⊙O外一点E.求证：BC=EC.

若，则锐角 ＝________．

下列数据：75，80，85，85，85，则这组数据的众数和中位数是　　

A．75，80 B．85，85 C．80，85 D．80，75

计算：．

已知函数的图像与x轴的交点坐标为且，则该函数的最小值是（　　　）

A.2 B.-2 C．10 D．-10

最近更新

　