初中 数学
A表示一个数,若把数A写成形如  的形式,其中
的形式,其中  、
、 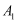 、
、  、
、  、…都为整数.则我们称把数A写成连分数形式.
、…都为整数.则我们称把数A写成连分数形式.
 的形式,其中
的形式,其中  、
、 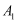 、
、  、
、  、…都为整数.则我们称把数A写成连分数形式.
、…都为整数.则我们称把数A写成连分数形式. 例如:把2.8写成连分数形式的过程如下:
2.8-2=0.8, 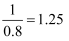 ,
,
1.25-1=0.25,  ,
,
4-4=0.
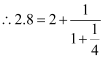
-
(1) 把3.245写成连分数形式不完整的过程如下:
3.245-3=0.245,
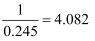 ,
,4.082-4=0.082,
 ,
,12.250-12=0.25,
 ,
,4-4=0.
∴

则
 ;
;  ;
; -
(2) 请把
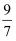 写成连分数形式;
写成连分数形式;
-
(3) 有这样一个问题:如图是长为47,宽为10的长方形纸片.从中裁剪出正方形,若长方形纸片无剩余,则剪出的正方形最少是几个?

小明认为这个问题和 “把一个数化为连分数形式” 有关联,并把
 化成连分数从而解决了问题.你可以参考小明的思路解决上述问题,请直接写出“剪出的正方形最少”时,正方形的个数.
化成连分数从而解决了问题.你可以参考小明的思路解决上述问题,请直接写出“剪出的正方形最少”时,正方形的个数.
如图,把平面内一条数轴  绕原点
绕原点  逆时针旋转角
逆时针旋转角  得到另一条数轴
得到另一条数轴  ,
,  轴和
轴和  轴构成一个平面斜坐标系.规定:过点
轴构成一个平面斜坐标系.规定:过点  作
作  轴的平行线,交
轴的平行线,交  轴于点
轴于点  ,过点
,过点  在
在  轴的平行线,交
轴的平行线,交  轴于点
轴于点  ,若点
,若点  在
在  轴上对应的实数为
轴上对应的实数为  ,点
,点  在
在  轴上对应的实数为
轴上对应的实数为  ,则称有序实数对
,则称有序实数对  为点
为点  的斜坐标.在某平面斜坐标系中,已知θ=60°,点
的斜坐标.在某平面斜坐标系中,已知θ=60°,点  的斜坐标为
的斜坐标为  ,点
,点  与点
与点  关于
关于  轴对称,则点
轴对称,则点  的斜坐标为.
的斜坐标为.
 绕原点
绕原点  逆时针旋转角
逆时针旋转角  得到另一条数轴
得到另一条数轴  ,
,  轴和
轴和  轴构成一个平面斜坐标系.规定:过点
轴构成一个平面斜坐标系.规定:过点  作
作  轴的平行线,交
轴的平行线,交  轴于点
轴于点  ,过点
,过点  在
在  轴的平行线,交
轴的平行线,交  轴于点
轴于点  ,若点
,若点  在
在  轴上对应的实数为
轴上对应的实数为  ,点
,点  在
在  轴上对应的实数为
轴上对应的实数为  ,则称有序实数对
,则称有序实数对  为点
为点  的斜坐标.在某平面斜坐标系中,已知θ=60°,点
的斜坐标.在某平面斜坐标系中,已知θ=60°,点  的斜坐标为
的斜坐标为  ,点
,点  与点
与点  关于
关于  轴对称,则点
轴对称,则点  的斜坐标为.
的斜坐标为.
如图,将抛物线y=−12x2平移得到抛物线m.抛物线m经过点A(6,0)和原点O,它的顶点为P,它的对称轴与抛物线y=−12x2交于点Q,则图中阴影部分的面积为.

如图是某几何体的表面展开图,则这个几何体是( )

A . 正三棱柱
B . 正方体
C . 圆柱
D . 圆锥
如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )

A . 130°
B . 140°
C . 150°
D . 160°
如图,在平面直角坐标系中,  ABCD的四个顶点分别为A(1,3),B(0,1),C(3,1),D(4,3)。
ABCD的四个顶点分别为A(1,3),B(0,1),C(3,1),D(4,3)。
 ABCD的四个顶点分别为A(1,3),B(0,1),C(3,1),D(4,3)。
ABCD的四个顶点分别为A(1,3),B(0,1),C(3,1),D(4,3)。 
-
(1) 作
 A1B1C1D1 , 使它与
A1B1C1D1 , 使它与  ABCD关于原点O成中心对称。
ABCD关于原点O成中心对称。
-
(2) 作
 A1B1C1D1的两条对角线的交点O1关于y轴的对称点O2 , 点O2的坐标为。
A1B1C1D1的两条对角线的交点O1关于y轴的对称点O2 , 点O2的坐标为。
-
(3) 若将点O2向上平移a个单位,使其落在
 ABCD内部(不包括边界),则a的取值范围是。
ABCD内部(不包括边界),则a的取值范围是。
—个多边形每个外角都是60°,此多边形一定是边形.
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2  ,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为.
,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为.
 ,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为.
,点P为AB边上的一个动点,连接PC,过点P作PQ⊥PC交BC边于点Q,则BQ的最大值为. 
同一平面内,一个点到圆的最小距离为  ,最大距离为
,最大距离为  ,则该圆的半径为
,则该圆的半径为 

 ,最大距离为
,最大距离为  ,则该圆的半径为
,则该圆的半径为 

A .  B .
B .  C .
C . 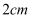 或
或  D .
D .  或
或 
 B .
B .  C .
C . 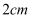 或
或  D .
D .  或
或 
下列命题是真命题的有( )个
①对顶角相等,邻补角互补;②两条直线被第三条直线所截,同位角的平分线平行;③垂直于同一条直线的两条直线互相平行;④过一点有且只有一条直线与已知直线平行。
A . 0
B . 1
C . 2
D . 3
已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )

A .  =
=  B .
B .  =
=  C . ∠B=∠D
D . ∠C=∠AED
C . ∠B=∠D
D . ∠C=∠AED
如图,△ABC≌△DEB,AB=DE,∠E=∠ABC,则∠C的对应角为.,BD的对应边为.

某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的重量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准重量的差值(单位:g) | -5 | -2 | 0 | 1 | 3 | 6 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
-
(1) 计算这批样品的平均重量,判断它比标准重量重还是轻多少?
-
(2) 若标准重量为450克,则这批样品的总重量是多少?
-
(3) 若这种食品的合格标准为450±5克,则这批样品的合格率为(直接填写答案)
我们把大树树干的横截面近似地看作一个圆,一棵大树树干的周长约是157厘米,求大树树干横截面的半径是多少厘米?
已知点  是直线
是直线  上一点,
上一点,  的横坐标为1,若点N与点
的横坐标为1,若点N与点  关于
关于  轴对称,则点N的坐标为( )
轴对称,则点N的坐标为( )
 是直线
是直线  上一点,
上一点,  的横坐标为1,若点N与点
的横坐标为1,若点N与点  关于
关于  轴对称,则点N的坐标为( )
轴对称,则点N的坐标为( )
A .  B .
B . 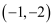 C .
C .  D .
D . 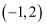
 B .
B . 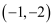 C .
C .  D .
D . 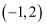
如图,一段公路的转弯处是一段圆弧( 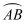 ),则
),则 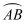 的展直长度为( )
的展直长度为( )
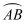 ),则
),则 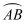 的展直长度为( )
的展直长度为( ) 
A . 3π
B . 6π
C . 9π
D . 12π
在Rt△ABC中,直角边AC=5,BC=12,则斜边AB上的高等于 。
试比较2a与3a的大小
计算:![]() 的结果是( )
的结果是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°,求坝底AD的长度.(精确到0.1米,参考数据:![]()
![]() ≈1.414,
≈1.414,![]()
![]() ≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比).
≈1.732.提示:坡度等于坡面的铅垂高度与水平长度之比).


最近更新
- 一张纸上画了一只鸡、一头牛和一片草地,要求把这三样东西分成两组,你会怎么分呢?实验表明,美国孩子更喜欢把鸡和牛分在一组,
- 若,则的值是 .
- 有A、B、C、D四种元素,A的原子核外有3个电子层,且第3电子层上的电子数比第2电子层的电子数少1;B元素的某氧化物分子
- The policy of the mainland is very clear and straightforward
- (2009湖南卷理)已知以双曲线C的两个焦点及虚轴的两个端点为原点的四边形中,有一个内角为60 ,则双曲线C的离心率为
- 1......
- 如图,两块相距d=6cm、水平放置的带电金属板,板长L=100cm,上板带正电,下板带负电.一质量m=1g、电荷量q=-
- 活跃在国际舞台上的国际组织,为数众多,类型不一。下列选填中均属于非政府国际组织的是 A.国际奥委会与国际红十字会
- 已知点P、A、B、C是球面上的四个点,PA、PB、PC两两垂直,且PA = PB=PC = 2,则A b两点间的球面距离
- “树欲静而风不止”,这句话反映了 ( ) A. 客观事物的存在与发展不以人的意志为转移 B. 世界上一切事物都是物
- 在知识经济时代,有人把国家区分为“脑袋国家”和“躯干国家”,“脑袋国家”通过生产和输出知识产权支配“躯干国家”,“躯干国
- 人们为了便于识别生物,生物学家编制出生物检索表,编制生物检索表的依据主要是() A. 生物生存环境的差异 B. 生物自身
- 阅读下面的材料,按照要求作文。(60分) 你要活得随意些,你就只能活得平凡些;你要活得辉煌些,你就只能活得痛苦些;你要活
- 阅读材料,回答下列问题。 贫困是世界各国和国际社会面临的挑战。促进发展,消除贫困,是人类孜孜以求的理想。 材
- 下列各句中加点的成语使用正确的一项是 A.诗歌到了《诗经》时代有了琴瑟的伴奏,更是洋洋大观了。 B.月明星稀,夜深人静,
- 两种短周期元素组成的化合物中,原子个数比为1:3,若两种元素的原子序数分别为a和b,则a和b的关系可能是( )
- 苏维埃政权颁布的法令规定:“必须实行国家的粮食垄断,即绝对禁止任何人的粮食贸易……绝对禁止任何人保存和隐藏粮食。”这一措
- 2009年12月16日,北京市发改委等部门举行了居民水价调整听证会。听证会共有25人参加,其中有22位参加人同意每立方米
- 关于物质和意识的关系正确的说法是: A. 精神是万能的,没有精神是万万不能的 B. 我们既要坚持物质决定论,又要坚持意识
- 动漫产业是指以“创意”为核心,以动画、漫画为表现形式,包含动漫图书、报刊、电影、电视、音像制品、舞台剧和基于现代侍播技术



