初中 数学
圣湖冬捕,世界奇观2017年1月1日查干湖冬捕26万公斤的惊人数字创下了单网冬捕产量新的吉尼斯世界纪录.将26万用科学记数法可表示为.
在实数  中,无理数有( )
中,无理数有( )
 中,无理数有( )
中,无理数有( )
A . 1
B . 2
C . 3
D . 4
已知⊙O 的直径为 4,AB 是⊙O 的弦,∠AOB=120°,点 P 在⊙O 上,若点 P到直线 AB 的距离为 1,则∠PAB 的度数为.
下列运算正确的是( )
A . (x-y)2=x2-y2
B . x6÷x2=x4
C . x2y+xy2=x3y3
D . x2·y2=(xy)4
下列图案中,既是轴对称图形,又是中心对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .
如图,等边 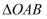 的边
的边  与
与  轴交于点
轴交于点  ,点
,点  是反比例函数
是反比例函数 
 图像上一点,若
图像上一点,若  为
为  边的三等分点时,则等边
边的三等分点时,则等边 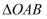 的边长为.
的边长为.
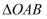 的边
的边  与
与  轴交于点
轴交于点  ,点
,点  是反比例函数
是反比例函数 
 图像上一点,若
图像上一点,若  为
为  边的三等分点时,则等边
边的三等分点时,则等边 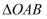 的边长为.
的边长为.
某品牌免洗洗手液按剂型分为凝胶型、液体型,泡沫型三种型号(分别用A,B,C依次表示这三种型号).小辰和小安计划每人购买一瓶该品牌免洗洗手液,上述三种型号中的每一种免洗洗手液被选中的可能性均相同.
-
(1) 小辰随机选择一种型号是凝胶型免洗洗手液的概率是.
-
(2) 请你用列表法或画树状图法,求小辰和小安选择同一种型号免洗洗手液的概率.
如图,钟表中9点30分时,时钟的分针与时针所成角的度数为.

如图,△ABC的三个顶点坐标分别是A(1,1),B(4,2),C(5,6).

( 1 )将△ABC向左平移7个单位长度后得到△A1B1C1 , 请作出△A1B1C1;
( 2 )△A2B2C2与△ABC关于坐标原点对称,则△A2B2C2的顶点坐标分别为A2( , ),B2( , ),C2( , );
( 3 )求△ABC的面积.
今年2月份,某市经济开发区完成出口316000000美元,将这个数据316000000用科学记数法表示应为( )
A . 316×106
B . 31.6×107
C . 3.16×108
D . 0.316×109
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=﹣ 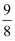 x2+bx+c的图象经过A、E两点,且点E的坐标为(﹣
x2+bx+c的图象经过A、E两点,且点E的坐标为(﹣  ,0),以0C为直径作半圆,圆心为D .
,0),以0C为直径作半圆,圆心为D .
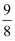 x2+bx+c的图象经过A、E两点,且点E的坐标为(﹣
x2+bx+c的图象经过A、E两点,且点E的坐标为(﹣  ,0),以0C为直径作半圆,圆心为D .
,0),以0C为直径作半圆,圆心为D . 
-
(1) 求二次函数的解析式;
-
(2) 求证:直线BE是⊙D的切线;
-
(3) 若直线BE与抛物线的对称轴交点为P , M是线段CB上的一个动点(点M与点B , C不重合),过点M作MN∥BE交x轴与点N , 连结PM , PN , 设CM的长为t , △PMN的面积为S , 求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.
天水市某中学为了解学校艺术社团活动的开展情况,在全校范围内随机抽取了部分学生,在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,围绕你最喜欢哪一项活动(每人只限一项)进行了问卷调查,并将调查结果绘制成如下两幅不完整的统计图.

请你根据统计图解答下列问题:
-
(1) 在这次调查中,一共抽查了名学生.
-
(2) 请你补全条形统计图.
-
(3) 扇形统计图中喜欢“乐器”部分扇形的圆心角为度.
-
(4) 请根据样本数据,估计该校1200名学生中喜欢“舞蹈”项目的共多少名学生?
9的平方根是( )
A . ±3
B . ﹣3
C . 3
D . 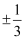
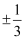
下列各式中,运算正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
今年“十一”长假某湿地公园迎来旅游高峰,第一天的游客人数是1.2万人,第三天的游客人数为2.3万人,假设每天游客增加的百分率相同且设为x,则根据题意可列方程为( )
A . 2.3 (1+x)2=1.2
B . 1.2(1+x)2=2.3
C . 1.2(1﹣x)2=2.3
D . 1.2+1.2(1+x)+1.2(1+x)2=2.3
 ;
;  .
.
若点P(a,b)在第三象限,则点Q(﹣a,b)一定在( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
如图通过将左图裁剪、用两块梯形拼接成右图,体现了什么数学公式( )

A . a2﹣b2=(a+b)(a﹣b)
B . (a﹣b)2=a2﹣2ab+b2
C . a(a+b)=a2+ab
D . (a+b)2=a2+2ab+b2
解不等式2x﹣3<![]() ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
![]()
若方程![]() 是关于
是关于![]() 的一元一次方程,则
的一元一次方程,则![]() 的值为( )
的值为( )
A.0 B.![]() C.1 D.
C.1 D.![]()
最近更新
- 求与曲线:相切,并且与直线:平行的直线方程。
- 读欧洲部分地区图,解答下列各题。(1)A表示的英法海底隧道位于英吉利海峡最窄处的___海峡。 (2)B表示的___地区中
- 右图所示装置可用于测定空气中氧气的含量,实验前在集气瓶内加入少量水,并做上记号。下列说法中不正确的是A.该实验证明空气中
- 在等差数列中,已知,那么= A. 2 B. 8 C. 18
- (2011年浙江温州,27题)为了纪念化学在自然科学领域取得的成就和贡献,联合国大会决定,将2011年定为“国际化学年”
- 要让权力在阳光下运行,发挥人民民主对权力的制约和监督,必须切实保障广大人民的 A、知情权、参与权与表达权 B、知情权
- —I’m sorry, sir. I didn’t mean to hurt you by showing you th
- 如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II
- 医院的化验科有时会将血液或尿液制作成临时玻片标本进行检查,从制作过程分,此类玻片标本属于() A.装片 B.切片 C.涂
- (2010广东理数)1.若集合A={-2<<1},B={0<<2}则集合A ∩ B=( ) A. {-1<<1}
- 下列是一些装置气密性的检查方法,其中正确的是()A.B.C.D.
- How about goingshopping on Hunan Road this evening? __
- (2011江苏无锡,19,4分) (−1)2 −+ (−2)0;
- 鸦片战争后,近代中国经济结构发生了很大变化。回答下面试题。 鸦片战争后,中国传统的经济结构最早受到冲击的地区是 A
- 乔治从美国芝加哥邮政大厦,给远在纽约的妈妈发了一封电报,电文如下:亲爱的妈妈:今天我要修理单位的电力系统,肯定要错过火车
- 北方地区的植被类型是( ) A.温带落叶阔叶林 B.亚热带常绿阔叶林 C.热带雨林
- 下列有关文学常识的表述错误的一项是( ) A.关汉卿、王实甫、白朴、马致远被称为“元曲四大家”,他们的代表作分别有
- DNA分子的一条链中(A+G)/(T+C)=0.4,上述比例在其互补链和整个DNA分子中分别是 A.0.4和0.6 B.
- herbs can help you to stay healthy. A.Eat B.Ea
- 食品安全与人类健康密切相关,下列做法不会危及人体健康的是( ) A.用“苏丹红一号”作食品添加剂



