初中 数学
如图,△ABC中,∠ABC,∠ACB的角平分线交于点O,过O点作MN∥BC分别交AB,AC于M,N两点,AB=7,AC=8,CB=9,则△AMN的周长是( )

 =.
=.
①-22÷(-2)3=1②-5÷  ×
×  =-25③-18÷6÷2=-6④-13-(-1)2=-2
=-25③-18÷6÷2=-6④-13-(-1)2=-2

 ,下列结论正确的是( )
,下列结论正确的是( )
 =-2
=-2  +3平行
D .
+3平行
D .  随
随  的增大而增大
的增大而增大

 )
D . (0,16)
)
D . (0,16)

-
(1) 在AC边上求作点E,使CE=2EA;(要求:尺规作图,不写作法,保留作图痕迹)
-
(2) 在(1)的条件下,若BC=12,求DE的长,

求证:
-
(1) △ADE≌△CDF.
-
(2) ME=NF.
 ,D、E分别是半径OA和OB的中点,求证:CD=CE.
,D、E分别是半径OA和OB的中点,求证:CD=CE. 

 的图象于点A,B,点C在反比例函数y=
的图象于点A,B,点C在反比例函数y=  (x>0)的图象上,连结CA,CB,当CA=CB且cos∠CAB=
(x>0)的图象上,连结CA,CB,当CA=CB且cos∠CAB=  时,k1 , k2应满足的数量关系是( )
时,k1 , k2应满足的数量关系是( )
 B .
B .  C .
C .  D .
D . 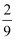

-
(1) 求∠FAD的度数;
-
(2) AB与ED有怎样的位置关系?为什么?
 ,则
,则  的值为( )
的值为( )
 x+4的图象与x轴、y轴分别相交于点A、B,四边形AOBC(O是原点)的一组对边平行,且AC=5.
x+4的图象与x轴、y轴分别相交于点A、B,四边形AOBC(O是原点)的一组对边平行,且AC=5. 
-
(1) 求点A、B的坐标;
-
(2) 求点C的坐标;
-
(3) 如果一个一次函数y=kx+b(k、b为常数,且k<0)的图象经过点A、C,求这个一次函数的解析式.
图 1 是某种路灯的实物图片,图 2 是该路灯的平面示意图, 










,
,



某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.如表是某周的生产情况(超产为正、减产为负):
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | ﹣2 | ﹣4 | +13 | ﹣10 | +16 | ﹣9 |
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行计件工资制,每辆车7元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
如图,△ABC内接圆于⊙O,∠B=30°,AC=2cm,则⊙O半径的长为_______cm.

先化简再求值:(![]()
![]() ﹣4)÷(x+1)•
﹣4)÷(x+1)•![]()
![]() ,其中x=
,其中x=![]()
![]() +1.
+1.
- 20.阅读下面的材料,根据要求写一篇不少于800字的文章。 英国《太阳报》曾以“世界上最大的快乐”为题,举办了一次有奖征
- 的展开式中,常数项为 .
- – Bob, ______ is it from your home toschool? – It’s about
- 阅读下面的文字,完成1-3题。 溴甲烷 溴甲烷,又称溴代甲烷或甲基溴,是一种无色无味的液体。它具有强烈的熏蒸作用,能杀灭
- 下列除去杂质的方法正确的是 物质 杂质 试剂 主要操作 A Cu Fe 盐酸 过滤 B CO2 CO O2 点燃
- — Do you think the weather is good enough for a picnic ? —
- 29. 关于辛亥革命与中国诞生的关系,指出:“研究中国的历史,还应该把党成立以前的辛亥革命和五四运动的材料研究一
- 被称之为“软电池”的纸质电池,采用一个薄层纸片作为传导体,在其一边镀锌,而在其另一边镀二氧化锰。在纸内的离子“流过”水
- 把重5N,体积为0.40dm3的物体投入水中,若不计水的阻力,当物体静止时,下列说法中正确的是g取10N/kg
- 友人要去远方,你去送别,友人哀伤愁苦,请你用《送杜少府之任蜀州》中的两句:“__________________,___
- 书面表达,根据汉语提示和要求写一篇短文。 要点: 1、现在越来越多的人喜欢养宠物,宠物正受到很多人的青睐。 2、养宠物有
- 为了探究石灰石与稀盐酸反应制备二氧化碳后的废液中的溶质成分,将废液过滤,取滤液20克于烧杯中,在不断振荡的条件下,向其中
- 下列各句中,没有语病且表意明确的一句是() A.这是一款待机功能十分突出的商务型手机,内置智能省电程序,能最大限度节约电
- 在浓盐酸中H3AsO3与SnCl2反应的离子方程式(未配平)为: SnCl2+Cl-+H3AsO3+H+ A
- “天安门上望,城下人如海。举头五角星,共庆山河改”,陈毅的这首诗记录了 A. 解放南京 B. 五四运动
- 有“地球之肺”和“地球之肾”之称的分别是() A.海洋生态系统和草原生态系统 B.海洋生态系统和湿地生态系统 C.草原生
- 已知在正项等比数列{an}中,a1=1, a2a4=16则|a1-12|+|a2-12|+…+|a8-12|=( )
- AttentionTim HortonsStainlessSteel Travel Mug OwnersLidRecal
- 下图是一种用于显示事物异同点的信息处理方法。图1中两个圆分别代表金刚石和石墨的有关信息,两圆重叠区域表示金刚石和石墨的共
- Do you want to live another 100 years or more? Some experts



