初中 数学
下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③  的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
A . ①②③
B . ③④⑤
C . ①②⑤
D . ②④⑤
如图,直线 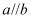 .则直线
.则直线  ,
,  之间的距离是( )
之间的距离是( )
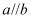 .则直线
.则直线  ,
,  之间的距离是( )
之间的距离是( ) 
A . 线段  的长度
B . 线段
的长度
B . 线段  的长度
C . 线段
的长度
C . 线段  D . 线段
D . 线段 
 的长度
B . 线段
的长度
B . 线段  的长度
C . 线段
的长度
C . 线段  D . 线段
D . 线段 
下列各组单项式中,是同类项的一组是( )
A . 3x2y与3xy2
B . 2abc与﹣3ac
C . ﹣2xy与yx
D . 2xy与2ab
某市居民生活用水实行“阶梯水价”收费,具体收费标准见下表:
|
每户每月用水量 |
水的价格(单位:元/吨) |
|
不超过20吨的部分 |
1.6 |
|
超过20吨且不超过30吨的部分 |
2.4 |
|
超过30吨的部分 |
3.3 |
例:甲用户1月份用水25吨,应缴水费  (元).
(元).
-
(1) 若乙用户1月份用水10吨,则应缴水费元;
-
(2) 若丙用户1月份应缴水费62.6元,则用水吨;.
-
(3) 若丁用户1、2月份共用水60吨(1月份用水量超过了2月份),设2月份用水
 吨,求丁用户1、2月份各应缴水费多少元.(用含
吨,求丁用户1、2月份各应缴水费多少元.(用含  的代数式表示)
的代数式表示)
-
(1) 计算:(-4b)·(-a2b)2÷(-2a);
-
(2) 分解因式:x2(x-2y)+xy2.
将两块大小相同的含30°角的直角三角板(∠BAC=∠B'A'C= 30° )按图①方式放置,固定三角板A'B'C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90° )至图②所示的位置,AB与A'C交于点E;AC与A'B'交于点F,AB与A'B'相交于点O。

-
(1) 求证:△BCE≌△B'CF。
-
(2) 当旋转角等于30°时,AB 与A'B'垂直吗?请说明理由。
如图,在平行四边形ABCD中,AB=2AD,M为AB的中点,连接DM,MC,BD.下列结论中:①DM⊥MC;②  ;③当DM=DA时,△DMN≌△CBN;④当∠DNM=45°时,
;③当DM=DA时,△DMN≌△CBN;④当∠DNM=45°时,  其中正确的结论是( )
其中正确的结论是( )
 ;③当DM=DA时,△DMN≌△CBN;④当∠DNM=45°时,
;③当DM=DA时,△DMN≌△CBN;④当∠DNM=45°时,  其中正确的结论是( )
其中正确的结论是( ) 
A . ①②③
B . ①③④
C . ①②④
D . ①②③④
若点  在第二象限,且点
在第二象限,且点  到
到  轴的距离为2,到
轴的距离为2,到  轴的距离为1,则点
轴的距离为1,则点  的坐标为( )
的坐标为( )
 在第二象限,且点
在第二象限,且点  到
到  轴的距离为2,到
轴的距离为2,到  轴的距离为1,则点
轴的距离为1,则点  的坐标为( )
的坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列说法中,错误的是( )
A . 对角线互相垂直平分的四边形是菱形
B . 平行四边形对角线的交点到一组对边的距离相等
C . 已知一次函数y=(a2+1)x﹣3,则y随x的增大而增大
D . 函数y=2x+b的图像不经过第二象限,则b<0
如图,抛物线  交
交  轴于点
轴于点  和点
和点  ,交
,交  轴于点
轴于点  .已知点
.已知点  的坐标为
的坐标为  ,点
,点  为第二象限内抛物线上的一个动点,连接
为第二象限内抛物线上的一个动点,连接  、
、  、
、  .
.
 交
交  轴于点
轴于点  和点
和点  ,交
,交  轴于点
轴于点  .已知点
.已知点  的坐标为
的坐标为  ,点
,点  为第二象限内抛物线上的一个动点,连接
为第二象限内抛物线上的一个动点,连接  、
、  、
、  .
. 

-
(1) 求这个抛物线的表达式.
-
(2) 当四边形
 面积等于4时,求点
面积等于4时,求点  的坐标.
的坐标.
-
(3) ①点
 在平面内,当
在平面内,当  是以
是以 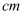 为斜边的等腰直角三角形时,直接写出满足条件的所有点
为斜边的等腰直角三角形时,直接写出满足条件的所有点  的坐标;
的坐标; ②在①的条件下,点
 在抛物线对称轴上,当
在抛物线对称轴上,当  时,直接写出满足条件的所有点
时,直接写出满足条件的所有点  的坐标.
的坐标.
在  中,
中,  .
.
 中,
中,  .
. 
-
(1) 如图①,若
 ,点
,点  分别在
分别在  上,将
上,将  沿
沿  折叠,使得点
折叠,使得点  与点
与点  重合,求折痕
重合,求折痕  的长;
的长;
-
(2) 如图②,点
 在
在  延长线上,且
延长线上,且  ,若
,若  ,求证:
,求证: 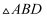 是直角三角形.
是直角三角形.
如图,直线  与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线  经过A,B.
经过A,B.
 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线  经过A,B.
经过A,B. 

-
(1) 求抛物线解析式;
-
(2) E(m,0)是x轴上一动点,过点E作
 轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
轴于点E,交直线AB于点D,交抛物线于点P,连接PB. ①点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标;
②点E在x轴的正半轴上运动,若
 ,请直接写出m的值.
,请直接写出m的值.
二次函数y=(x+1)2 , 与x轴交点坐标为( )
A . (—1,0)
B . (1,0)
C . (0,—1)
D . (0,1)
阅读下列材料:
问题:如何计算  呢?
呢?
小明带领的数学活动小组通过探索完成了这道题的计算.他们的解法如下:
解:原式 


请根据阅读材料,完成下列问题:
-
(1) 计算:
 ;
;
-
(2) 计算:
 ;
;
-
(3) 利用上述方法,求式子
 的值.
的值.
某种服装原价每件150元,经两次降价,现售价每件96元.若设该服装平均每次降价的百分率为x,则可列出关于x的方程为.
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=  (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的表达式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的表达式为y=k2x+b.
 (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的表达式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的表达式为y=k2x+b. 
-
(1) 求反比例函数和直线EF的表达式;
-
(2) 求△OEF的面积;
-
(3) 请结合图象直接写出不等式k2x+b-
 >0的解集.
>0的解集.
在△ABC中,AB=5,BC=6,B为锐角且sinB= , 则∠C的正弦值等于( )
, 则∠C的正弦值等于( )
 , 则∠C的正弦值等于( )
, 则∠C的正弦值等于( )
A . 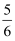 B .
B .  C .
C .  D .
D . 
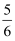 B .
B .  C .
C .  D .
D . 
下列各式能用平方差公式分解因式的是( )
A . m2+n2
B . 4x2﹣(﹣y2)
C . ﹣4a2﹣b2
D . ﹣9x2+4y2
底面周长为10πcm,高为12cm的圆锥的侧面积为.
如图,一次函数![]() 与二次函数
与二次函数![]() 的图象相交于A(
的图象相交于A(![]() ,5)、B(9,2)两点,则关于
,5)、B(9,2)两点,则关于![]() 的不等式
的不等式![]() 的解集为
的解集为
(A) ![]() ( B)
( B) ![]() (C)
(C) ![]() ( D)
( D) ![]() 或
或![]()

最近更新
- One man was to meet his wifedowntown and spend some time sho
- 8.下列各组句子中加横线词活用现象不同的一项是( ) A.而后乃今将图南/目吴会于云间 B.眄庭柯以怡颜/策扶老以流
- 某实验小组利用拉力传感器和速度传感器探究“动能定理”.如实图5-3所示,他们将拉力传感器固定在小车上,用不可伸长的细线将
- “微博营销”是一种新兴营销方式,强调以客户为中心,在正确的时间把正确的信息传递给正确的人,它以微博为营销平台,向听众(
- 测得某DNA片段含有碱基1600个,其中腺嘌呤占27.5%,问该DNA复制两次需要游离的鸟嘌呤脱氧核苷酸有多少个(
- 铝土矿是一种用口呵气后会发出强烈土臭味的矿石,主要含Al2O3·H2O、Al2O3·3H2O以及少量Fe2O3、SiO2
- 已知R2+离子核外有a个电子,b个中子。表示R原子符号正确的是( ) A. B. C.
- 在平行四边形ABCD中,∠A=,边AB,AD的长分别为2,1.若M,N分别是边BC,CD上的点,且满足=,则·的取值范围
- 阅读下面的古诗,回答问题。(4分)田园乐王维桃红复含宿雨,柳绿更带朝烟。花落家童未扫,莺啼山客犹眠。【小题1】王维的诗“
- 金属钠中的钠原子和氯化钠中的钠离子都属钠元素,原因是( ) A、具有相同的电子数 B、具有相同
- 一切真理只有经历下面三个阶段才会被人接受:第一阶段,觉得可笑而不加理会;第二阶段,视为邪说而强烈抗拒;第三阶段,未加思索
- 如图10,在△ABC中,DE∥BC,DE与边AB相交于点D,与边相交于点E,如果AD=6,BD=8,AE=4,那么CE
- 一位母亲记录了儿子3—9岁的身高,数据(略),由此建立的身高与年龄的回归模型为,用这个模型预测这个孩子10岁时的身高
- “在这一群优秀的人物中间所主张的学说是:这个有形的世界是上帝以爱来创造的,是 在上帝心中先有的一个模型的仿制,上帝将永
- 下列外出旅游常见病症及应备药品的组合,正确的是 ()。 A.高血压病人——硝酸甘油片 B.冠心病患者——防暑药 C.易晕
- —Look at the girl with a pair of glasses over there. Can you
- 已知命题, 则为 ▲ .
- Tsinghua University, _____in 1911, is home to a great number
- 用下列实验装置完成对应的实验(部分仪器巳省略),能达到实验目的的是( )
- (08年芜湖一中二模)仿照下面划线的句子再写一句语义相近的句子。(5分)心正则笔直。宋代抗金名将岳飞,精忠报国,一心收复



