初中 数学
如图,把一长方形纸片沿  折盈后,点
折盈后,点  、
、  分别落在
分别落在 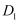 、
、  的位置,若
的位置,若  ,则
,则  等于( )
等于( )
 折盈后,点
折盈后,点  、
、  分别落在
分别落在 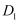 、
、  的位置,若
的位置,若  ,则
,则  等于( )
等于( ) 
A . 65º
B . 62º
C . 56º
D . 64º
计算
-
(1) (﹣12)﹣5+(﹣18)﹣(﹣35)
-
(2)

-
(3)

-
(4)

-
(5)

-
(6)

因式分解: =
=
 =
=
在  ,
, 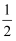 ,0,﹣2这四个数中,为无理数的是( )
,0,﹣2这四个数中,为无理数的是( )
 ,
, 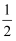 ,0,﹣2这四个数中,为无理数的是( )
,0,﹣2这四个数中,为无理数的是( )
A .  B .
B . 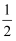 C . 0
D . ﹣2
C . 0
D . ﹣2
 B .
B . 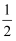 C . 0
D . ﹣2
C . 0
D . ﹣2
一个商贩准备了10张质地均匀的纸条,其中能得到一块糖的纸条有5张,能得到三块糖的纸条有3张,能得到五块糖的纸条有2张.从中随机抽取一张纸条,恰好是能得到三块糖的纸条的概率是.
若m>n,则下列各式正确的是( )
A . m+4<n+4
B . 6m<6n
C . ﹣5m<﹣5n
D . 3m﹣1<3n﹣1
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB, 则∠BAD的度数为( )
A . 30°
B . 35°
C . 40°
D . 50°
若等式 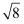 □
□  =4成立,则□内的运算符号是( )
=4成立,则□内的运算符号是( )
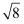 □
□  =4成立,则□内的运算符号是( )
=4成立,则□内的运算符号是( )
A . +
B . ﹣
C . ×
D . ÷
﹣  的绝对值是( )
的绝对值是( )
 的绝对值是( )
的绝对值是( )
A . ﹣  B .
B .  C .
C .  D . ±
D . ± 
 B .
B .  C .
C .  D . ±
D . ± 
某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:  ;
;  ;
;  ;
;  ,并绘制出如图不完整的统计图.
,并绘制出如图不完整的统计图.
 ;
;  ;
;  ;
;  ,并绘制出如图不完整的统计图.
,并绘制出如图不完整的统计图. 
解答下列问题:
-
(1) 求被抽取的学生成绩在
 组的有多少人?
组的有多少人?
-
(2) 所抽取学生成绩的中位数落在哪个组内?
-
(3) 学校要将D组最优秀的4名学生分成两组,每组2人到不同的社区进行“交通法规”知识演讲.已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,求九年级的2名学生恰好分在同一个组的概率.
﹣  的相反数是( )
的相反数是( )
 的相反数是( )
的相反数是( )
A .  B . ﹣6
C . 6
D . ﹣
B . ﹣6
C . 6
D . ﹣ 
 B . ﹣6
C . 6
D . ﹣
B . ﹣6
C . 6
D . ﹣ 
已知关于工的不等式3x-m+1>0的最小整数解为2,则实数m的取值范围是.
下列计算正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知△ABC≌△A′B′C′,若∠A=50°,∠B′=80°,则∠C的度数是( )
A . 30°
B . 40°
C . 50°
D . 60°
计算:
-
(1)

-
(2)
 (精确到0.01)
(精确到0.01)
方差是刻画数据波动程度的量,对于一组数据x1,x2,x3,xn,可用如下算式计算方差:  ,其中“5”是这组数据的( )
,其中“5”是这组数据的( )
 ,其中“5”是这组数据的( )
,其中“5”是这组数据的( )
A . 最小值
B . 平均数
C . 中位数
D . 众数
已知|a|=2,|b|=3,且在数轴上表示有理数b的点在a的左边,则a﹣b的值为( )
|
| A. | ﹣1 | B. | ﹣5 | C. | ﹣1或﹣5 | D. | 1或5 |
下列各式计算正确的是 【 】
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
如图,点E为正方形ABCD边AB上运动,点A与点F关于DE对称,作射线CF交DE延长线于点P,连接AP、BF.
(1)若∠ADE=15°,求∠DPC的度数;
(2)试探究AP与PC的位置关系,并说明理由;
(3)若AB=2,求BF的最小值.

①
如图①,直线AB与x轴负半轴、y轴正半轴分别交于A、B两点.OA、OB的长度分别为a和b,且满足
![]() .
.
⑴判断△AOB的形状.
②
⑵如图②,正比例函数
![]() 的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长.
的图象与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=9,BN=4,求MN的长.
⑶如图③,E为AB上一动点,以AE为斜边作等腰直角△ADE,P为BE的中点,连结PD、PO,试问:线段PD、PO是否存在某种确定的数量关系和位置关系?写出你的结论并证明.
 |
最近更新
- 农科所技术员研究温度对某蔬菜新品种产量的影响,将实验结果绘制成如下曲线。据此提出以下结论,你认为合理的是A.光合作用酶的
- the morning he often runs. But yesterdaymorning he
- 关于细胞分化的叙述,正确的是 ( ) A.已分化的细胞都是不可逆转的 ,遗传物质发生了改变。 B.细胞分化
- 等于什么数时,式子与的值相等。
- 阅读下列材料:(10分) 材料一图示一 图示二 材料二
- 下列正确的叙述有()① CO2、NO2、P2O5均为酸性氧化物 ② Ca(HCO3)2、Fe(OH)3、FeCl2均可由
- 东京也无非是这样。上野的樱花烂熳的时节,望去确也像绯红的轻云,但花下也缺不了成群结队的“清国留学生”的速成班,头顶上盘着
- 22.春节期间,在北京工作的小张收到了二叔的儿子(在北京读大学)带来的土特产,他很高兴,给二叔写了一封信,但其中有5个词
- 细菌在15N培养基中繁殖数代后,使细菌DNA的含氮碱基皆含有15N,然后再移入14N培养基中培养,抽取亲代及子代的DNA
- 在同样大小的两张图纸上,分别绘制一幅凉山州地图和世界地图,两幅地图选用比例尺 的情况应是( )
- 选修4-5:不等式选讲 (本小题满分10分) 设a、b是非负实数,求证:。
- 用显微镜观察紫色洋葱表皮细胞时,一般看不到染色体,这是因为( ) A.紫色液泡干扰了观察
- 两只相同的电阻,分别通以正弦波形的交流电和方波形的交流电,两种交流电的最大值相等,且周期相等.在正弦波形交流电的一个周期
- 下列关于科学研究和实验方法的叙述,不正确的是() A.摩尔根等人通过假说—演绎法,证实了基因在染色体上 B.“建立血糖调
- 抢救大面积烧伤病人和严重贫血病人时,应该分别输给 A.鲜血和红细胞 B.血浆和红细胞 C.血浆和白细胞
- Wendy hurried to the airport, only ______ the pop singer had
- 我国的全国人大代表,来自各地区、各民族、各行业,工人、农民、知识分子、解放军和妇女、归国华侨等都有适当的比例,人口再少的
- Dear Editor, I used to be a doctorin the children’s dep
- Sally’s father is ill in hospital. and her mother has to loo
- 战后初期,有人站在德国首都柏林的街头,望着满目废墟的城市,哀叹即使清理这些瓦砾也要二十年时间,要复兴比登天还难,然而,西



