下列计算正确的是（   ）

如图，在△ABC中，∠BAD＝∠DAC ， DF⊥AB ， DM⊥AC ， AF＝10cm ， AC＝14cm ， 动点E以2cm/s的速度从A点向F点运动，动点G以1cm/s的速度从C点向A点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t．

数轴上A、B两点分别表示- 和-3，那么A、B两点的距离是（   ）

若α为锐角，且  sin(α-10°）= ， 则α等于（   ）

已知点A（a，2）在一次函数y=x+1的图象上，则a= 

如图，已知直线 ，直线m,n与直线a,b,c分别交于点 则 ．

如图，正六边形ABCDEF内接于⊙O，若AB=2，则⊙O的半径为．

下列命题中，真命题是（   ）

若关于x的一元二次方程（k﹣1）x²+2x﹣2=0有两个不相等的实数根，则k的取值范围是 

如图，在锐角△ABC中，AB＝2，AC＝ ，∠ABC＝60°.D是平面内一动点，且∠ADB＝30°，则CD的最小值是

已知任一平面封闭图形，现在其外部存在一水平放置的矩形，使得矩形每条边都与该图形有至少一个交点，且构成该图形的所有点都在矩形内部或矩形边上，那么就称这个矩形为“该图形的矩形”，且这个矩形的水平长成为该图形的宽，铅直高称为该图形的高.如图，边长为1的菱形的一条边水平放置，已知“该菱形的矩形”的“高”是“宽”的 ，则该“菱形的矩形”的“宽”为.

如图所示，在四边形 中， ， 为 的中点，连接 、 ， ，延长 交 的延长线于点 ．求证：

在学习《圆》这一章时，老师给同学们布置了一道尺规作图题．

尺规作图：过圆外一点作圆的切线．

已知： 为 外一点．

求作：经过点 的 的切线．

小敏的作法如下：

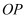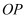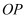①连接 ，作线段 的垂直平分线 交 于点 ；

②以点 为圆心， 的长为半径作圆，交 于 两点；

③作直线 ．所以直线 就是所求作的切线．

根据小敏设计的尺规作图过程．

榴莲是热带著名水果之一，榴莲营养极为丰富，含有蛋白质、糖类、多种维生素、膳食纤维、脂肪、叶酸，氨基酸和矿物质，有强身健体、滋阴补阳之功效.它的气味浓烈、爱之者赞其香，厌之者怨其臭，喜欢榴莲的人也喜欢榴莲干，榴莲千层，榴莲披萨、榴莲酥等榴莲加工制品，某校数学兴趣小组为了了解本校学生喜爱榴莲的情况，随机抽取了200名学进行问卷调查，经过统计后绘制了两幅尚不完整的统计图.（注：每一位同学在任何一种分类统计中只有一种选择）

请根据统计图完成下列问题：

如图，已知∠1＝∠2＝∠3＝55º，则∠4＝（    ）

如图，若要使平行四边形ABCD成为菱形，需添加的条件是（   ）

绝对值最小的数是；绝对值等于本身的数是；绝对值是它的相反数的数是.

若a，b互为相反数，c，d互为倒数，m的绝对值是5，则代数式-a+(-cd)²⁰²⁰-b+m的值为。