高二数学试题
已知![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 的直线与抛物线交于不同的两点
的直线与抛物线交于不同的两点![]() ,与圆
,与圆![]() 交于不同的两点
交于不同的两点![]() (如图),则
(如图),则![]() 的值是( )
的值是( )
A.![]() B.2 C.1 D.
B.2 C.1 D.![]()

已知实数![]() 满足
满足 ,则
,则![]() 的最大值为
的最大值为
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
设函数![]() ,若对于
,若对于![]() ,
,![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是 。
的取值范围是 。
不论m为何实数,直线![]() 恒过的定点坐标是______________.
恒过的定点坐标是______________.
若![]()
![]() ,则
,则![]() 直线
直线![]() 不经过第 象限.
不经过第 象限.
![]() 的展开式中
的展开式中![]() 的系数为 ( )
的系数为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知动圆![]() 经过点
经过点![]() ,
,![]() .
.
(1)求周长最小的圆的一般方程;
(2)求圆心在直线![]() 上的圆的标准方程.
上的圆的标准方程.
.设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x <0时,f ′(x)g(x)+f(x)g′(x)>0,且![]() ,则不等式f(x)g(x)<0的解集是( )
,则不等式f(x)g(x)<0的解集是( )
A. (-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
我校为了解学生喜欢通用技术课程“机器人制作”是否与学生性别有关,采用简单随机抽样的办法在我校高一年级抽出一个有60人的班级进行问卷调查,得到如下的![]() 列联表:
列联表:
| 喜欢 | 不喜欢 | 合计 | |
| 男生 | 18 | ||
| 女生 | 6 | ||
| 合计 | 60 |
已知从该班随机抽取1人为喜欢的概率是![]() .
.
(Ⅰ)请完成上面的![]() 列联表;
列联表;
(Ⅱ)根据列联表的数据,若按90%的可靠性要求,能否认为“喜欢与否和学生性别有关”?请说明理由.
参考临界值表:
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
把命题“![]() ”的否定写在横线上__________.
”的否定写在横线上__________.
关于![]() 的一元二次不等式
的一元二次不等式![]() 的解集为
的解集为![]() ,
,
则![]() 的值为( )
的值为( )
A.-6 B.-5 C.6 D.5
在单位正方体![]() 中,
中,![]() 是
是![]() 的中点,如图建立空间直角坐标系.
的中点,如图建立空间直角坐标系.
(1)求证![]() ∥平面
∥平面![]() .
.
(2)求异面直线![]() 与
与![]() 夹角的余弦值.
夹角的余弦值.
 (3)求直线
(3)求直线![]() 到平面
到平面![]() 的距离.
的距离.
已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)证明:![]() (
(![]() 为自然对数的底)恒成立.
为自然对数的底)恒成立.
若![]() 是正实数,且
是正实数,且![]() ,
,![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 时等号成立,利用以上结论,可以得到函数
时等号成立,利用以上结论,可以得到函数![]() 的最小值为__ ,
的最小值为__ ,
取得最小值时![]() 的值为 .
的值为 .
若抛物线![]() 的准线经过双曲线
的准线经过双曲线![]() 的一个焦点,则
的一个焦点,则![]() _____.
_____.
已知![]() ,则
,则![]() ,函数
,函数![]() 的零点的个数为 .
的零点的个数为 .
用秦九韶算法求多项式f(x)=6![]() +5
+5![]() +3
+3![]() +2
+2![]() +x当x=2时的值时,
+x当x=2时的值时,![]() =________.
=________.
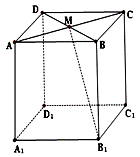
在长方体ABCD—A1B1C1D1中, M为AC与BD的交点,若![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() 则下列向量中与
则下列向量中与![]() 相等的向量是( )
相等的向量是( )
A. ![]() B.
B. ![]()
B. C. ![]() D.
D. ![]()
向量![]() =(2,4,x),
=(2,4,x),![]() =(2,y,2),若|
=(2,y,2),若|![]() |=6,且
|=6,且![]() ⊥
⊥![]() ,则x+y的值为
,则x+y的值为![]() ( )
( )
A.-3 B.1 ![]() C
C![]() .-3或1 D.3或1
.-3或1 D.3或1
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯 ( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
- 下列对变法或改革的评价与(1)(4)人物(看图),均无关的是( ) ①促进了社会经济的发展 ②使原有社会
- 水量盈余率是衡量水库蓄水量变化的重要指标(水量盈余率=流入量/流出量)。下图为北半球某水库各月水量盈余率统计图。读图回答
- 组成酶化学成分的基本单位是 ( ) ①蛋白质 ②DNA ③脱氧核苷酸 ④氨基酸 ⑤核糖核苷酸
- 阅读下面这首宋诗,完成(1)~(2)题。春 日 吴锡畴① 韶光大半去匆匆,几许幽情递不通。 燕未成家寒食雨,人如中酒落花
- 如图1,在中,,,,另有一等腰梯形()的底边与重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.1.直接写
- “某物体由静止开始在t时间内运动了S的路程”,仅凭这段描述,你只能得到( )
- 下图是二战后日本经济发展总量柱状图,导致这一状况的原因是( ) ①美国的扶植 ②战后政治民主化改革
- 如图所示,三条平行等距的虚线表示电场中的三个等势面,电势值分别为10V、20V、30V,实线是一带负电的粒子(不计重力)
- 墨子说:“尽也农夫之所以早出暮入,强乎耕稼树艺,多聚菽粟,而不敢怠倦者,何也?曰:彼以为强必富,不强必贫;强必饱,不强必
- 在氮化硅中添加氧化铝,用氧原子取代一部分氮,用铝原子取代一部分硅,通过常压烧结即成为新一代无机非金属材料,叫氧氮化硅铝,
- In spite of repeated wrongs done to him, he looks _____ to p
- 在“研究平抛运动”实验中,某同学只记录了小球运动途中的A、B、C三点的位置,取A点为坐标原点,则各点的位置坐标如图所示,
- 当前世界交通运输的发展趋势是 ( ) ①提高运
- 下列由左到右的变形哪 是因式分解,哪 不是(是的打“∨”,不是的打“×”): a3-b3=(a-b)(a2+ab+b2
- (12分)如图所示,A、B为两块平行金属薄板,A板带正电、B板带负电。两板之间存在着匀强电场,两板间距为d、电势差为U,
- All her life, my mother wanted busy children. It was very im
- 下列反应中,既属于离子反应,又属于有颜色变化的氧化还原反应的是( ) A.FeCl3溶液和KSCN溶
- 根据相关知识回答下列问题: (1)实验开始时,关闭K1,开启K2和分液漏斗活塞,滴加苯和液溴的混合液,反应开始。过一会儿
- 下列加点的成语使用不正确的一项是( ) A、这些第三代移民,在物质方面已经西化,但在精神方面,祖国母亲赋予他们的文化底蕴
- I saw him______ the game on the computer yesterday evening.



