高二数学试题
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样的方法(按A类、B类分两层)从该工厂的工人中抽取100名工人,调查他们的生产能力(此处生产能力![]() 指一天加工的零件数),结果如下表.
指一天加工的零件数),结果如下表.
表1:A类工人生产能力的频数分布表
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 8 | x | 3 | 2 |
表2:B类工人生产能力的频数分布表
| 生产能力分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 人数 | 6 | y | 27 | 18 |
(1)确定x,y的值;
(2)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.001的前提下认为工人的生产能力与工人的类别有关系?
| 生产能力分组 工人类别 |
|
| 总计 |
| A类工人 | |||
| B类工人 | |||
| 总计 |
(3)工厂规定生产零件数在![]() 的工人为优秀员工,在
的工人为优秀员工,在![]() 的工人为模范员工,那么在样本的A类工人中的优秀员工和模范员工中任意抽2人进行示范工作演示,试写出所抽的模范员工的人数X的分布列和期望。
的工人为模范员工,那么在样本的A类工人中的优秀员工和模范员工中任意抽2人进行示范工作演示,试写出所抽的模范员工的人数X的分布列和期望。
下面的临界值表仅供参考:
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
已知向量![]() ,则向量
,则向量![]() 的夹角的余弦值为________.
的夹角的余弦值为________.
设函数![]() ,则
,则![]() ( )
( )
A.2 B.-2 C.5 D.![]()
等比数列![]() 中,
中,![]() ,则数列
,则数列![]() 的前8项和等于( )
的前8项和等于( )
A.6 B.5 C.4 D.3
已知函数![]() ,则下列结论正确的是
,则下列结论正确的是
A. f(x)的最小正周期为![]()
B. f(x)的最小值为-2
C.直线![]() 为函数f(x)图象的一条对称轴
为函数f(x)图象的一条对称轴
D.将函激f(x)的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象
的图象
已知![]() ,
,![]() 。
。
(1)求![]() 的单调区间;
的单调区间;
(2)若对于任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设函数![]() ,其中
,其中![]() ,求函数
,求函数![]() 在
在![]() 上的最小值.
上的最小值.
已知![]() 是
是![]() 上的一个随机数,则使
上的一个随机数,则使![]() 满足
满足![]() 的概率为 .
的概率为 .
某船开始看见灯塔在南偏东30![]() 方向,后来船沿南偏东60
方向,后来船沿南偏东60![]() 的方向航行45km后,看见灯塔在正西方向,则这时船与灯塔的距离是 .
的方向航行45km后,看见灯塔在正西方向,则这时船与灯塔的距离是 .
已![]() 知f(x)=xlnx,g(x)=x3+ax2﹣x+2.
知f(x)=xlnx,g(x)=x3+ax2﹣x+2.
(1)求函![]() 数f(x)的单调区间;
数f(x)的单调区间;
(2)对任意x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(x元)试销![]() 天,得到如表单价x(元)与销量y(册)数据:
天,得到如表单价x(元)与销量y(册)数据:
| 单价x(元) | 18 | 19 | 20 | 21 | 22 |
| 销量y(册) | 61 | 56 | 50 | 48 | 45 |
(1)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]()
函数![]() 在区间
在区间![]() 上的平均变化率为( )
上的平均变化率为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
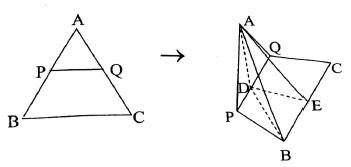
正三角形![]() 的边长为
的边长为![]() ,将它沿平行于
,将它沿平行于![]() 的线段
的线段![]() 折起(其中
折起(其中![]() 在边
在边![]() 上,
上,![]() 在
在![]() 边上),使平面
边上),使平面![]() 平面
平面![]() 。
。![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若折叠后,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,求
,求![]() 最小时,四棱锥
最小时,四棱锥![]() 的体积.
的体积.
给出下列命题: ①函数y=sin x![]() 的图像与y=x的图像有三个交点;
的图像与y=x的图像有三个交点;
②函数![]() 是偶函数;③若
是偶函数;③若![]() 是第一象限的角,且
是第一象限的角,且![]() ,则
,则![]() ;
;
④直线![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
⑤函数![]() 的图像关于点
的图像关于点![]() 成对称中心图形.
成对称中心图形.
⑥若![]() ,则
,则![]() 其中
其中![]()
其中正确命题的序号是 .
曲线![]() 在点
在点![]() 处的切线倾斜角为( )
处的切线倾斜角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知函数![]() ,
,![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() 是增函数,设
是增函数,设![]() ,
,
![]() ,
,![]() ,则
,则![]() 、
、![]() 、
、![]() 的大小顺序是( )。
的大小顺序是( )。
![]() .
. ![]()
![]() .
. ![]()
![]() .
. ![]()
![]() .
. ![]()
在数列![]() 中,
中,![]() ,则
,则![]()
设![]() 为实数时,实数
为实数时,实数![]() 的值是 .
的值是 .
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60 C.120 D.140

△ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB.
(1)求B.(2)若b=2,求△ABC面积的最大值.
在100个零件中,有一级品20个、二级品30个、三级品50个,从中抽取20个作为样本.
①将零件编号为00,01,…,99,抽签取出20个;
②采用系统抽样法,将所有零件分成20组,每组5个,然后每组中随机抽取1个;
③采用分层抽样法,从一级品中随机抽取4个,从二级品中随机抽取6个,从三级品中随机抽取10个.
对于上述问题,下面说法正确的是( )
A.不论采用哪一种抽样方法,这100个零件中每一个被抽到的概率都是![]()
B.①②两种抽样方法,这100个零件中每一个被抽到的概率为![]() ,③并非如此
,③并非如此
C.①③两种抽样方法,这100个零件中每一个被抽到的概率为![]() ,②并非如此
,②并非如此
D.采用不同的抽样方法,这100个零件中每一个零件被抽到的概率是各不相同的
- 按下列的题目要求在图16的平面直角坐标系上画出相应的点和线段,已知每个方格的 边长都为1. (1)在平面直角坐标系中描出
- 从四川省核电站发展论坛上传出消息:四川首家核电站项目已经确定选址,预计2010年开建,2014年投入使用.该项目建成后,
- 有A、B、C、D四种金属,投入水中只有D反应放出氢气,将A投入C的盐溶液中可置换出金属C,B的最高价氧化物的水化物碱性比
- 对英国“光荣革命”意义理解错误的是( ) A.极大地提高了英国议会权威 B.使英国确立了责任
- Thecar was full, but I managed to ______ in. A.arrive
- 已知一个角的补角加上10º后等于这个角余角的3倍,则这个角为___
- 下图甲示缩手反射相关结构,图乙是图甲中某一结构亚显微结构模式图,据图回答:(1)甲图中f表示的结构是 ,乙图是甲图中__
- 有两种不同的铀原子,一种原子核内有92个质子和143个中子,另一种原子核内有92个质子和146个中子,则它们不相等的是
- 已知程序框图如图,若输入的x值分别为0,1,2,执行该程序后,输出的y的值分别为a,b,c,则a+b+c=.
- 为缓解北京区的旱情,有关部门选择适宜的条件和方法,向大气中发射催雨剂。其主要成分是干冰、液氮、碘化银等。下列有关叙述不正
- 商鞅变法措施中,对后世政治体制影响最为深远的是 A.废井田,开阡陌 B.奖励耕织 C.按军功授爵 D.建立县
- 阅读下面的文字,完成下列各题(共16分) 太史公牛马走司马迁再拜言。少卿足下:…… 古者富贵而名摩灭,不可胜记,唯倜傥非
- 假设双氧水(H2O2)是比碳酸还弱的二元酸。</PGN0031A.TXT/PGN> (1)双氧水电离的方程式
- 纵一苇之所如,__________________。(苏轼《赤壁赋》)
- 一根绝缘细线下栓一带电小球A,细线的上端固定在天花板上,在悬点正下方某一适当位置,固定另一带种电荷的小球B,由于库仑斥力
- --- My name is Rebecca. Shall I spell it for you? ---
- (本小题满分14分) 已知函数的极大值点为. (1)用实数来表示实数,并求的取值范围; (2)当时,的最小值为,求的值;
- 下图为电镜下观察的某细胞的一部分。下列有关该细胞的叙述中,正确的是A.此细胞既可能是真核细胞也可能是原核细胞 B.此细胞
- (2015•如东县一模)在研究物质的导电性时,采用如图所示的实验电路.用酒精灯对着取自白炽灯的玻璃芯柱加热,灯泡L会慢慢
- (1)取0.2 mol·L-1 HCl溶液与0.2 mol·L-1 MOH溶液等体积混合(忽略混合后溶液体积的变化),测



