高二数学试题
如图,斜三棱柱![]() 中,侧面
中,侧面![]() 为菱形,底面
为菱形,底面![]() 是等腰直角三角形,
是等腰直角三角形,![]() .
.
(1)求证:直线![]() 直线
直线![]() ;
;
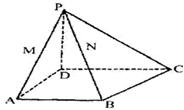 (2)若直线
(2)若直线![]() 与底面
与底面![]() 成的角为60°,求二面角
成的角为60°,求二面角![]() 的余弦值.
的余弦值.
(1.05)6的计算结果精确到0.01的近似值是( )
A. 1.23 B. 1.24 C. 1.33 D. 1.34
有一段演绎推理是这样的“若直线平行于平面,则该直线平行于平面内所有直线;已知直线![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]() ∥直线a”,这显然是错误的,这是因为( )
∥直线a”,这显然是错误的,这是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
某厂生产甲产品每吨需用原料![]() 和原料
和原料![]() 分别为2吨和3吨,生产乙产品每吨需用原料
分别为2吨和3吨,生产乙产品每吨需用原料![]() 和原料
和原料![]() 分别为2吨和1吨.甲、乙产品每吨可获利润分别为3千元和2千元.现有12吨原料
分别为2吨和1吨.甲、乙产品每吨可获利润分别为3千元和2千元.现有12吨原料![]() ,8吨原料
,8吨原料![]() .问计划生产甲产品和乙产品各多少吨才能使利润总额达到最大.
.问计划生产甲产品和乙产品各多少吨才能使利润总额达到最大.
某城市随机抽取一年(365天)内1![]() 00天的空气质量指数API的监测数据,结果统计如下:
00天的空气质量指数API的监测数据,结果统计如下:
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气 质量 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中度 重污染 | 重度 污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为w)的关系式为:
S=
试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染.完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
| 非重度污染 | 重度污染 | 总计 |
| 供暖季 |
|
|
|
| 非供暖季 |
|
|
|
| 总计 |
|
| 100 |
附:![]()
|
| 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
国庆期间,我校高三(1)班举行了社会主义核心价值观知识竞赛,某轮比赛中,要求参赛者回答全部5道题,每一道题回答正确记1分,否则记﹣1分.据以往统计,甲同学能答对每一道题的概率均为![]() .甲同学全部回答完这5道题后记他的得分为X
.甲同学全部回答完这5道题后记他的得分为X
(1)求X=1的概率;
(2)记随机变量Y=|X|,求Y的分布列和数学期望.
若圆C:x2+y2-4x-4y-10=0上至少有三个不同的点到直线l:x-y+c
=0的距离为2![]() ,则c的取值范围是( )
,则c的取值范围是( )
A.[-2![]() ,2
,2![]() ] B.(-2
] B.(-2![]() ,2
,2![]() ) C.[-2,2] D.(-2,2)
) C.[-2,2] D.(-2,2)
盒中装有10个乒乓球,其中6个新球,4个旧球,不放回地依次取出2个球使用,在第一次取出新球的条件下,第二次也取到新球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
若直角坐标平面内的两点![]() 满足条件:(1)
满足条件:(1)![]() 都在函数
都在函数![]() 的图象上;(2)
的图象上;(2)![]() 关于原点对称.则称点对
关于原点对称.则称点对![]() 是函数
是函数![]() 的一对“友好点对”(点对
的一对“友好点对”(点对![]() 与
与![]() 看作同一对“友好点对”).已知函数
看作同一对“友好点对”).已知函数![]() ,则此函数的“友好点对”的个数为_______.
,则此函数的“友好点对”的个数为_______.
已知x+y+z=1.
![]() 证明:(1)x2+y2+z2≥xy+yz+zx,
证明:(1)x2+y2+z2≥xy+yz+zx,
(2)x2+y2+z2![]()
![]() .
.
函数![]() 的单调减区间为(
的单调减区间为(![]() ,0)
,0)
(1)求![]() 的值;
的值;
(2)求过点P(0,0)且与f(x)相切的直线方程。
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
 (2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
命题P:![]() ,
,![]() ,写出命题P的否定
,写出命题P的否定![]() P:_______________
P:_______________
如图,在正方体ABCDA1B1C1D1中, 棱长为2,M,N分别为A1B,AC的中点.
(1)证明:MN// B1C;
(2)求A1B与平面A1 B1CD所成角的大小.
 |
已知直角![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,直角顶点
,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴上.
轴上.
(Ⅰ)求边![]() 所在直线的方程;
所在直线的方程;
(Ⅱ)求三角形![]() 的斜边中线所在的直线的方程.
的斜边中线所在的直线的方程.
以抛物线![]() 的顶点为圆心的圆交
的顶点为圆心的圆交![]() 于
于![]() 两点,交
两点,交![]() 的准线于
的准线于![]() 两点.已知
两点.已知![]() ,
,![]() ,则
,则![]() 的焦点到准线的距离为
的焦点到准线的距离为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
设F1,F2分别是椭圆C:![]() +
+![]() =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直.直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直.直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为![]() ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
“1<x<2”是“x<2”成立的________条件.
在一次考试中,5名学生的数学和物理成绩如下表:(已知学生的数学和物理成绩具有线性相关关系)
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |
现已知其线性回归方程为![]() =0.36x+
=0.36x+![]() ,则根据此线性回归方程估计数学得90分的同学的物理成绩为________(四舍五入到整数).
,则根据此线性回归方程估计数学得90分的同学的物理成绩为________(四舍五入到整数).
设函数![]() ,
,![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的单调递减区间和极值;
的单调递减区间和极值;
(2)若对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
- 中东和平进展在很大程度上取决于两大宗教之间的相互谅解,这两大宗教是 A.伊斯兰教与基督教
- 靛蓝是一种食品用合成色素,但对人体有害。使用时必须严格控制使用量。靛蓝允许小于0.1g·kg-1。靛蓝结构简式如图所示。
- Why does teaching as a career ______ many people? A. apply f
- 常温下,若溶液中由水电离产生的c(OH-)=1×10-14mol·L-1,满足此条件的溶液中一定可以大量共存的离子组是
- 下列说法不正确的是A.从海带中提取碘单质的过程涉及氧化还原反应B.往淡水中加入NaCl等配成人造海水,可用于海产品的长途
- According to the air traffic rules, you ______ switch off yo
- 为缓解城市公交运输压力,我校综合实践活动小组针对我市淮海路交通拥挤现象,设计电力机车专用道。同学们收集到电力机车和公交汽
- 下列关于自然界中氮循环(如下图)的说法不正确的是()A.氮元素均被氧化 B.工业合成氨属于人工固氮 C.含氮无机物和含氮
- 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F. (1)求证
- 下列各物质所含原子数目,按由大到小顺序排列的是() ①0.5mol NH3 ②标准状况下22.4L氦气 ③4℃9mL
- 图中甲乙表述两种商品的价格和数量之间的关系。对此理解正确的是( )A.大米、蔬菜的价格与需求关系符合甲 B.甲商品的销量
- (顺义24)某同学对下列四个实验都设计了两种方案,其中方案1合理、方案2不合理的是 实验目的 方案1 方案2A清洗铁制
- 下列离子方程式与所述事实相符且正确的是A.在亚磷酸(结构式为)中加入过量的烧碱溶液: H3PO3+3OH-=PO33-+
- 下列物质的用途主要与其化学性质有关的是------------------------------( ) A、铜
- 仔细观察图中动物,回答下列问题:(1)A、B与C、D、E、F的主要区别是身体背部没有 。
- 已知集合,,则等于( ) {,1} []
- (2009年广东卷文)已知平面向量a= ,b=, 则向量 A.平行于轴 B.平行于第一、三
- 水平路面上有一个重500 N的小车,在100 N的水平拉力作用下,匀速向前移动了5 m,则在这一过程中A.车受到的阻力为
- (09德州)在元旦联欢晚会上,被誉为化学魔术师的晓慧同学为同学们表演了一组化学魔术,在三支盛有液体的玻璃杯中,分别倒入用
- (本小题满分12分) 在边长为的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、



