函数的图象大致是（   ）

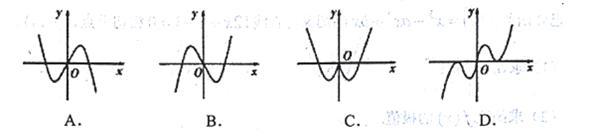
空间四边形OABC中，OA=6,AB=4,AC=3,BC=6，∠OAC＝∠OAB＝，则cos〈，〉等于(　　)

A.          B.        C．        D．

钝角三角形ABC 的面积是，AB=1,BC=,则AC等于（   ）

A．5　　　　B．     C．2    D．1

已知是所在平面外一点，是的中点，若，则（    ）

A.-1                   B. 0                   C.                 D. 1

已知f(x)＝x³＋ax²＋(a＋6)x＋1有极大值和极小值，则a的取值范围为__________．

已知y＝f（x）是定义在R上的奇函数，且x<0时，f（x）＝1＋2^x．

（1）求函数f（x）的解析式．

（2）画出函数f（x）的图象．

（3）写出函数f（x）单调区间及值域．

已知a≥0，函数f(x)＝(x²－2ax)e^x，若f(x)在[－1，1]上是单调减函数，则a的取值范围是(　  　)A．0<a<          B．<a<           C．a≥         D．0<a<

直线被曲线截得的弦长为            ;

y＝x－ln(1+x)的单调递增区间是 ( )

A．( -1 ,0 )    B．( -1 ,+)    C．(0 ,+)    D．(1 ,+)

如表是降耗技术改造后生产甲产品过程中记录的产量（吨）与相应的生产能耗（吨标准煤）的几组对应数据，根据表中提供的数据，求出关于的回归直线方程为，则表中的值为

A．           B．          C.           D．

二次函数f（x）的图象经过点（0，），且f′（x）=﹣x﹣1，则不等式f（10^x）＞0的解集为（　　）

A．（﹣3，1）     B．（﹣lg3，0）   C．（，1） D．（﹣∞，0）

从某市的中学生中随机调查了部分男生，获得了他们的身高数据，整理得到如下

频率分布直方图．

（1）求的值并估计该市中学生中的全体男生的平均身高（假设同组中的每个数据用该组区间的中点值代替）；

（2）从该市的中学生中随机抽取一名男生，根据直方图中的信息，估计其身高在180以上的概率．若从全市中学的男生（人数众多）中随机抽取3人，用表示身高在180以上的男生人数，求随机变量的分布列和数学期望．

已知首项的数列满足，则数列的前项和__________．

以抛物线的焦点为圆心,且过坐标原点的圆的方程为（    ）

A．     B．

C．       D．

如图，矩形的两条对角线相交于点，边所在直线的方程为，点在边所在直线上．

(Ⅰ)求边所在直线的方程

(Ⅱ)求矩形外接圆的方程

已知是椭圆（）的左，右焦点，直线与该椭圆交于，若 是直角三角形，则该椭圆的离心率为

A．            B．           C．            D．或

两条直线y=ax-2与y=x+1互相垂直，则a等于　（    ）

    A.2                 B.1                 C. -1               D. 0   

命题“，”的否定是（   ）

A．，        B．，

C．，           D．，

已知f（x）=mx2+nx﹣2（n＞0，m＞0）的图象与x轴交与（2，0），则的最小值为

在数列中，，若为等差数列，

若 ，求Tn.