高二数学试题
一个三位数的百位,十位,个位上的数字依次是a,b,c,当且仅当![]() 时称为“凹数”,若
时称为“凹数”,若![]() ,从这些三位数中任取一个,则它为“凹数”的概率是( )
,从这些三位数中任取一个,则它为“凹数”的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知![]() ,则“
,则“![]() 且
且![]() ”是“
”是“![]() ”的( )
”的( )
A. 充要条件 B. 必要非充分条件 C. 充分非必要条件 D. 既非充分也非必要条件
命题![]() ,则方程
,则方程![]() 表示椭圆,命题
表示椭圆,命题![]() 函数
函数![]() 的图象过定点
的图象过定点![]() ,则下列命题
,则下列命题
A. ![]() 假 B.
假 B. ![]() 真 C.
真 C. ![]() 真,
真,![]() 假 D.
假 D. ![]() 假,
假,![]() 真
真
如图,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6。
⑴ 求证:平面![]() 平面ACD;
平面ACD;
⑵ 求二面角![]() 的平面角的正切值;
的平面角的正切值;
⑶ 设过直线AD且与BC平行的平面为![]() ,求点B到平面
,求点B到平面![]() 的距离。
的距离。

某厂生产某种电子元件,如果生产出一件正品,可获利200元,如果生产出一件次品,则损失100元.已知该厂制造电子元件过程中,次品率p与日产量x的函数关系是:p=![]() (x∈N+).
(x∈N+).
(1)写出该厂的日盈利额T(元)与日产量x(件)的函数关系式;(用x表示T)
(2)为获取最大日盈利,该厂的日产量应定为多少件?
△ABC的内角A,B,C的对边分别为a,b,c,已知![]() .
.
(Ⅰ)求角C;
(Ⅱ)若c=![]() ,△ABC的面积为
,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
 如图,在四棱锥
如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ∥
∥![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,
![]()
(1)若![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,试求
,试求![]() 的值.
的值.
设质点做直线运动,已知路程![]() 是时间
是时间![]() 的函数
的函数![]() ,则质点在
,则质点在![]() 时的瞬时速度为 .
时的瞬时速度为 .
已知 ![]() 是函数
是函数 ![]() 的极小值点,那么函数
的极小值点,那么函数 ![]() 的极大值为( )
的极大值为( )
A.15 B.16 C.17 D.18
在![]() 中,角
中,角![]() 所对应的边分别为
所对应的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,
, ![]() 的面积为
的面积为![]() ,求该三角形的周长.
,求该三角形的周长.
若![]() ,
, ![]() 满足约束条件
满足约束条件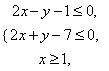 则
则![]() 的取值范围为__________.
的取值范围为__________.
![]()
已知椭圆C:![]() 经过点M(1,
经过点M(1,![]() ),其离心率为
),其离心率为![]() ,设直线
,设直线
![]() 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线![]() 与圆
与圆![]() 相切,求证:OA⊥OB(O为坐标原点).
相切,求证:OA⊥OB(O为坐标原点).
已知函数![]()
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若对任意![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 的取值范围为______.
的取值范围为______.
椭圆![]() 的焦距为
的焦距为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
如图,已知![]() ,
,![]() 是
是![]() 的中点,沿直线
的中点,沿直线![]() 将
将![]() 翻折
翻折
成![]() ,所成二面角
,所成二面角![]() 的平面角为
的平面角为![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()

某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
| 1.47 | 20.6 | 0.78 | 2.35 | 0.81 | −19.3 | 16.2 |
 表中
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的
的斜率和截距的
最小二乘法估计值分别为
已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满足不等式![]() +2ax0+2a≤0,若命题“p或q”是假命题,求a的取值范围.
+2ax0+2a≤0,若命题“p或q”是假命题,求a的取值范围.
抛物线![]() 的准线方程是 .
的准线方程是 .
- 空气中含量最多的物质是( ) A.氧气 B.氮气 C.水
- 新中国建立后,我国的义学艺术事业受到党和国家的重视。党中央提出“百花齐放,百家争鸣”的方针是在什么时候? A.1953年
- 下列哪种活动不利于大气环境保护: ( )A、大
- 下列物质中,其形成与内质网上的核糖体、内质网、高尔基体、线粒体都有关系的是( )A.血红蛋白 B.染色体上的蛋
- (12分)如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发
- 阅读下面的内容,完成下面3题 反智主义主宰社会固然不好,但一个没有反智主义的社会,也同样成问题。有人说中国历代的专制皇权
- . O2F2可以发生反应:H2S+4O2F2=SF6+2HF+4O2,下列说法正确的是 A..氧气是氧化产物
- 2013年,我国继续实施积极的财政政策和稳健的货币政策。下列措施中符合“积极的财政政策”的是( ) 中国人民银行安排
- 下列关于仪器使用的说法正确的是 A.在量取液体后,量筒中残留的液体要用蒸馏水洗涤并转入相应容器 B.熔融纯碱、烧碱时,不
- 完形填空Mike was the best table tennis player in his school and
- “诸侯朝于天子,曰述职,述职者,述所职也。无非事者……一不朝则贬其爵,再不朝则削其地,三不朝则六师移之。”这种制度应该
- 如图4,一次函数的图象与反比例函数的图象交于P(-2,1)、Q(1,)两点. (1)求反比例函数和一次函数的解析式; (
- 2008年12月15日,海协会与海基会11月在台北签署的有关协议正式生效,两岸海运直航、空运直航、直接通邮全面启动,宣告
- 在用电火花计时器“研究匀变速直线运动”的实验中,如图所示的是一次记录小车运动情况的纸带,图中A、B、C、D、E为相邻的计
- If man’s best friend is a dog, then who isa dog’s best frien
- She __________ (实现,完成) her ambition.
- 用NA表示阿伏加德罗常数的值,下列叙述中正确的是 A. 含有NA个氦原子的氦气在标准状况下的体积约为11.2L B. 2
- 下列不属于商业银行主要业务的选项是 A.吸收存款 B.发行股票 C.发放货款
- 做平抛运动的物体,某时刻在竖直方向和水平方向的分速度大小相等,则该时刻物体到抛出点的水平距离和竖直距离之比为: A.1:
- 罗斯福新政通过立法规定工人最低工资和最高工时的目的是() A.克服经济危机,稳定资本主义制度 B.争取工人支持,建立社会



