圆形磁场 知识点题库
如下图所示,在半径为R的圆形区域内充满磁感应强度为B的匀强磁场,MN是一竖直放置的感光板。从圆形磁场最高点P垂直磁场射入大量的带正电,电荷量为q,质量为m,速度为v的粒子,不考虑粒子间的相互作用力,关于这些粒子的运动以下说法正确的是( )
 ,沿不同方向入射的粒子出射后均可垂直打到MN上
,沿不同方向入射的粒子出射后均可垂直打到MN上
如图所示,半径为r的圆形空间内,存在着垂直于纸面向里的匀强磁场,一个带电粒子(不计重力),从A点以速度v0垂直磁场方向射入磁场中,并从B点射出,∠AOB=1200 , 则该带电粒子在磁场中运动的时间为( )
 πr/3v0
C . πr/3v0
D .
πr/3v0
C . πr/3v0
D .  πr/3v0
πr/3v0

回旋加速器的工作原理如题15-1图所示,置于真空中的D形金属盒半径为R,两盒间狭缝的间距为d,磁感应强度为B的匀强磁场与盒面垂直,被加速粒子的质量为m,电荷量为+q,加在狭缝间的交变电压如题15-2图所示,电压值的大小为Ub。周期T=  。一束该粒子在t=0- 时间内从A处均匀地飘入狭缝,其初速度视为零。现考虑粒子在狭缝中的运动时间,假设能够出射的粒子每次经过狭缝均做加速运动,不考虑粒子间的相互作用。求:
。一束该粒子在t=0- 时间内从A处均匀地飘入狭缝,其初速度视为零。现考虑粒子在狭缝中的运动时间,假设能够出射的粒子每次经过狭缝均做加速运动,不考虑粒子间的相互作用。求:

①出折粒子的动能  ;②粒子从飘入狭缝至动能达到
;②粒子从飘入狭缝至动能达到  所需的总时间
所需的总时间 ![]() ;
;
③要使飘入狭缝的粒子中有超过99%能射出,d应满足的条件.
如图所示,圆形区域半径为R,内有一垂直纸面的匀强磁场,磁感应强度的大小为B1 , P为磁场边界上的一点,相同的带正电的粒子,以相同的速率从P点射入磁场区域,速度方向沿位于纸面内的各个方向.这些粒子射出磁场边界的位置在边界的某一段弧上.这段圆弧的弧长是圆周的  ,若将磁感应强度的大小变为B2 , 结果相应的弧长变为圆周长的
,若将磁感应强度的大小变为B2 , 结果相应的弧长变为圆周长的  ,不计粒子的重力和粒子间的相互影响,则( )
,不计粒子的重力和粒子间的相互影响,则( )

 R
B . 磁感应强度的大小变为B2时粒子轨迹半径为R
C .
R
B . 磁感应强度的大小变为B2时粒子轨迹半径为R
C .  =
= 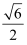 D .
D .  =
= 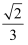
如图所示,一圆柱形匀强磁场区域的横截面为半径为R的圆,磁感应强度大小为B,方向垂直于纸面向外.一质量为m、电荷量为q的带负电的粒子沿垂直于直径ab的方向射入磁场区域,入射点与ab的距离为 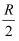 ,已知粒子出射时速度方向偏转了60°(不计重力).则粒子的速率为( )
,已知粒子出射时速度方向偏转了60°(不计重力).则粒子的速率为( )

 B .
B .  C .
C .  D .
D . 

-
(1) 若粒子在筒内未与筒壁发生碰撞,求该粒子的荷质比和速率分别是多大?
-
(2) 若粒子速率不变,入射方向在该截面内且与MN方向成30°角,则要让粒子与圆筒无碰撞地离开圆筒,圆筒角速度应为多大?

 t
C .
t
C .  t
D . 2t
t
D . 2t

 B .
B .  C .
C .  D .
D . 
 =2cm,两金属板通过导线与宽度为L1=0.5m的金属导轨相连,导轨处在垂直纸面向里的匀强磁场中,磁感应强度为B1=1T.有一长为L2=1m的导体棒放在导轨上,导体棒与导轨接触良好且始终与导轨垂直.现对导体棒施一力F,使导体棒以v1=8m/s匀速向右运动.有一比荷
=2cm,两金属板通过导线与宽度为L1=0.5m的金属导轨相连,导轨处在垂直纸面向里的匀强磁场中,磁感应强度为B1=1T.有一长为L2=1m的导体棒放在导轨上,导体棒与导轨接触良好且始终与导轨垂直.现对导体棒施一力F,使导体棒以v1=8m/s匀速向右运动.有一比荷 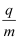 =5×107C/kg的粒子(不计重力)从M板处由静止释放,经过小孔S,沿SA进入圆形磁场,求:
=5×107C/kg的粒子(不计重力)从M板处由静止释放,经过小孔S,沿SA进入圆形磁场,求:
-
(1) 导体棒两端的电压;
-
(2) M、N之间场强的大小和方向;
-
(3) 粒子在离开磁场前运动的总时间(计算时取π=3).
 C/kg的带正电的粒子,若沿y轴正方向射入磁场的粒子恰能从磁场最右侧的A点沿x轴正方向垂直进入电场,不计粒子的重力及粒子间的相互作用和其他阻力.求:
C/kg的带正电的粒子,若沿y轴正方向射入磁场的粒子恰能从磁场最右侧的A点沿x轴正方向垂直进入电场,不计粒子的重力及粒子间的相互作用和其他阻力.求: 
-
(1) 粒子源发射的粒子进入磁场时的速度大小;
-
(2) 沿y轴正方向射入磁场的粒子从射出到打到荧光屏上的时间(计算结果保留两位有效数字);
-
(3) 从O点处射出的粒子打在荧光屏上的纵坐标区域范围.

 ,则粒子从P关于圆心的对称点离开时的运动时间是最长的
C . 若粒子射入的速率为
,则粒子从P关于圆心的对称点离开时的运动时间是最长的
C . 若粒子射入的速率为 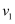 时,这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速率为
时,这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速率为 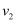 ,相应的出射点分布在三分之一圆周上,则
,相应的出射点分布在三分之一圆周上,则  D . 若粒子在磁场边界的出射点分布在六分之一圆周上,打在磁场边界最远位置粒子的运动时间为
D . 若粒子在磁场边界的出射点分布在六分之一圆周上,打在磁场边界最远位置粒子的运动时间为  ;若粒子在磁场边界的出射点分布在三分之一圆周上,打在磁场边界最远位置粒子的运动时间为
;若粒子在磁场边界的出射点分布在三分之一圆周上,打在磁场边界最远位置粒子的运动时间为  ,则
,则 
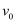 垂直磁场射入,当该电荷离开磁场时,速度方向刚好改变了180°,不计电荷的重力,下列说法正确的是( )
垂直磁场射入,当该电荷离开磁场时,速度方向刚好改变了180°,不计电荷的重力,下列说法正确的是( ) 
 D . 该点电荷的比荷
D . 该点电荷的比荷 
 ,当粒子在加速腔
,当粒子在加速腔  中运动时腔内能产生加速电场,加速电压
中运动时腔内能产生加速电场,加速电压  ,细管道
,细管道  的长度
的长度  ,其内部将磁场屏蔽,
,其内部将磁场屏蔽,  点位于
点位于  的正上方、
的正上方、  间的距离
间的距离  。氦核由静止注入到加速腔,在加速腔加速后,以水平速度垂直于
。氦核由静止注入到加速腔,在加速腔加速后,以水平速度垂直于  进入磁场,经过多次回旋加速后,恰好从
进入磁场,经过多次回旋加速后,恰好从  点进入管道,并沿管道做匀速直线运动,从
点进入管道,并沿管道做匀速直线运动,从  点离开加速器。忽略加速腔的大小,不计氦核的重力和氦核在加速腔中运动的时间。(氦核质量
点离开加速器。忽略加速腔的大小,不计氦核的重力和氦核在加速腔中运动的时间。(氦核质量  、电荷量
、电荷量  )
) 
-
(1) 试判断匀强磁场的方向;
-
(2) 求氦核从细管道飞出时的动能
 ;
;
-
(3) 求氦核从静止开始运动到
 点的总时间
点的总时间  。
。

-
(1) 求加速电场场强E0的大小;
-
(2) 求匀强磁场的磁感应强度B的大小;
-
(3) 若仅将该圆形区域的磁场改为平行于纸面的匀强电场,如图乙所示,带电粒子垂直射入该电场后仍然从N点射出。求该匀强电场场强E的大小。
 时间从C点射出磁场,OC与OB成60°角。现只改变带电粒子的速度大小,仍从A点沿原方向射入磁场,粒子在磁场中的运动时间变为1.5
时间从C点射出磁场,OC与OB成60°角。现只改变带电粒子的速度大小,仍从A点沿原方向射入磁场,粒子在磁场中的运动时间变为1.5  , 不计粒子重力,则粒子的速度大小变为( )
, 不计粒子重力,则粒子的速度大小变为( ) 
 B .
B .  C .
C .  D .
D . 
 ,
,  ,电子质量为m,电荷量为e,忽略电子间相互作用。
,电子质量为m,电荷量为e,忽略电子间相互作用。 
-
(1) 求磁感应强度B的大小;
-
(2) 求电子流从P点射出时与负y轴方向的夹角θ的范围;
-
(3) 满足(2)的前提下,定性画出电流i随UAK变化的关系曲线。要求标出相关数据,且要有计算依据。

 的圆,与y轴相切于点
的圆,与y轴相切于点  ,圆内有匀强磁场,方向垂直于xOy平面向外。在
,圆内有匀强磁场,方向垂直于xOy平面向外。在  处有一个比荷为
处有一个比荷为  的带正电的粒子,正对该圆圆心方向发射,粒子的发射速率
的带正电的粒子,正对该圆圆心方向发射,粒子的发射速率  ,粒子在Q点进入第一象限。在第一象限某处存在一个矩形匀强磁场区域,磁场方向垂直于xOy平面向外,磁感应强度
,粒子在Q点进入第一象限。在第一象限某处存在一个矩形匀强磁场区域,磁场方向垂直于xOy平面向外,磁感应强度  。粒子经该磁场偏转后,在x轴M点
。粒子经该磁场偏转后,在x轴M点  沿y轴负方向进入第四象限(不考虑粒子的重力)。求:
沿y轴负方向进入第四象限(不考虑粒子的重力)。求: 
-
(1) 第二象限圆内磁场的磁感应强度B的大小。
-
(2) 第一象限内矩形磁场区域的最小面积。
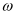 (未知)匀速转动,求:
(未知)匀速转动,求:

-
(1)
 的大小;
的大小;
-
(2) 考虑实际情况,粒子在狭缝中运动的时间不能忽略,求粒子从飘入狭缝一直加速至动能达到最大的过程中,粒子在狭缝中的加速时间
 ;
;
-
(3) 在第(2)问情景下,要使飘入的粒子有99%能射出,求狭缝宽度d满足的条件。
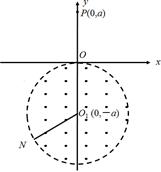
-
(1) 判断粒子的带电性质
-
(2) 求带电粒子的比荷(电量与质量之比)
-
(3) 若在粒子从 O 点运动到 N 点的过程中,某时刻磁感应强度大小突然变化为 B ,粒子不再离开磁场,求 B
的最小值
- —I hope I can get better grades this time. _________. You
- 材料:A市在经济迅速增长的同时,也发生了
- 为了把2008年北京奥运会办成“绿色”奥运,
- 用同样大小的黑色五角星按如图所示的方式摆
- 某剧院前贴出一张海报,上写“豹子头刊金印
- It was not a serious illness, and she soon____ it. �
- 实验课上老师要求设法了解氢氧化钠溶液逐滴
- 物质的量就像一座桥梁,将物质的
- 计算:【小题1】(I) 【小题2】(II) 【小
- 观察下图,判断发生在M点的战役是 (
- 已知水稻高秆(T)对矮秆(t)为显性,抗病
- 1. They are waiting for you at the bus s______.2. Beijing i
- 下列句子没有语病的一句是 ( ) A.这一
- 关于物态变化,下列现象属于熔化的是
- 下列词语中加线字读音全正确的一项是(
- 1992年,欧共体12国正式签署《欧洲联盟条约》
- 公元前5世纪剧作家阿里斯托芬提到,雅典政
- 一物体静止在光滑的水平桌面上,现对其施加
- 读图完成下列各题。假设甲、乙、丙三地有三



