2 中位数与众数 知识点题库
| 最高气温(℃) | 25 | 26 | 27 | 28 |
| 天 数 | 1 | 1 | 2 | 3 |
则这组数据的中位数与众数分别是( )
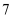 名学生的中考体育分数如下:
名学生的中考体育分数如下:  ,
, 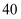 ,
,  ,
,  ,
, 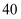 ,
,  ,
, 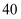 ,该组数据的众数、中位数分别为( )
,该组数据的众数、中位数分别为( )
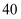 ,
,  B .
B . 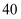 ,
,  C .
C .  ,
, 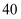 D .
D . 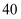 ,
, 

|
时间分段/min |
频数/人数 |
频率 |
|
10~20 |
8 |
0.200 |
|
20~30 |
14 |
a |
|
30~40 |
10 |
0.250 |
|
40~50 |
b |
0.125 |
|
50~60 |
3 |
0.075 |
|
合计 |
c |
1.000 |

-
(1) 这里采用的调查方式是;
-
(2) 求表中a、b、c的值,并请补全频数分布直方图;
-
(3) 在调查人数里,等候时间少于40min的有人;
-
(4) 此次调查中,中位数所在的时间段是~min.
|
跳绳成绩(个) |
132 |
133 |
134 |
135 |
136 |
137 |
|
一班人数(人) |
1 |
0 |
1 |
5 |
2 |
1 |
|
二班人数(人) |
0 |
1 |
4 |
1 |
2 |
2 |
-
(1) 两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:
众数
中位数
平均数
方差
一班
a
135
135
c
二班
134
b
135
1.8
表中数据a=,b=,c=;
-
(2) 请用所学的统计知识,从两个角度比较两个班跳绳比赛的成绩.

-
(1) 根据图示补全下表;
平均数(分)
中位数(分)
众数(分)
A队
83
85
B队
95
-
(2) 结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好;
-
(3) 计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定。
 ,得到一组新数据
,得到一组新数据  ,
,  ,
,  ,
, 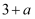 ,
,  ,这两组数据的以下统计量相等的是( )
,这两组数据的以下统计量相等的是( )

-
(1) 本次接受随机抽样调查的学生人数为,图①中
 的值为;
的值为;
-
(2) 求本次调查获取的样本数据的众数、中位数和平均数;
-
(3) 根据样本数据,估计该校一周的课外阅读时间大于
 的学生人数.
的学生人数.
 ,
, 另外 给出了部分信息如下:
甲班 10 名学生的成绩:99,80,99,86,99,96,90,100,89,82.
乙班 10 名学生的成绩在 C 组的数据:94,90,94.
| 甲乙两班被抽取学生成绩统计表 | ||
| 班级 | 甲班 | 乙班 |
| 平均数 | 92 | 92 |
| 中位数 | 93 | a |
| 众数 | b | 100 |
| 方差 | 52 | 50.4 |

根据以上信息,解答下列问题:
-
(1) 上面图表中的a=,b=.扇形统计图中“D 组”所对应的圆心角的度数为;
-
(2) 甲乙两班共有 120 名学生参加了此次定时练习,估计成绩为较好的学生有多少人.
为防疫防控需要,某校师生积极接种该疫苗,历时一个月至2021年1月19日,该校师生已有大部分接种该疫苗,市卫健委为了掌握该校师生接种该疫苗后的适应情况,更好的追踪后期数据反馈,特从该校七年级和八年级各随机抽取20个班级,对班级接种人数情况进行收集,整理,分析后,给出以下信息:
七年级20个班级各班级接种人数:
45,28,36,32,47,45,52,48,43,54,
52,40,52,38,41,52,46,48,51,49.
八年级20个班级各班级接种人数条形统计图:

抽取的七年级,八年级的班级接种人数的平均数,众数,中位数及接种达到或超过50人的班级数所占全年级抽样的班级百分比情况,如下表所示:
| 年级 | 平均数 | 众数 | 中位数 | 接种达到或超过50人的班级所占全年级抽样的班级百分比情况 |
| 七年级 | 44.95 | a | 46.5 | 30% |
| 八年级 | 48.30 | 47 | b | c% |
根据以上信息,解答以下问题:
-
(1) 直接写出上表中a,b,c的值:
 ;
;  ;
;  ;
;
-
(2) 你认为该校七年级,八年级的接种情况,哪个年级的接种情况更好?请说出你的理由;
我认为(填“七年级”或“八年级”)的接种情况更好;理由是(只填一个):;
-
(3) 接种人数达到或超过50人的班级,视为“防控特别积极”,若该校有120个班级,试估算该校“防控特别积极”的班级有多少个?

 ;B:
;B:  ;C:
;C:  ;D:
;D:  ,并绘制出如下不完整的统计图:
,并绘制出如下不完整的统计图: 
-
(1) 填空:n=;
-
(2) 补全频数分布直方图;
-
(3) 抽取的这n名学生成绩的中位数落在组;
-
(4) 若规定学生成绩
 为优秀.估算全校成绩达到优秀的人数.
为优秀.估算全校成绩达到优秀的人数.
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
|
60 |
70 |
80 |
90 |
100 |
|
|
1班 |
0 |
1 |
6 |
2 |
1 |
|
2班 |
1 |
1 |
3 |
4 |
1 |
|
3班 |
1 |
1 |
4 |
2 |
2 |
分析数据:
|
平均数 |
中位数 |
众数 |
|
|
1班 |
83 |
80 |
80 |
|
2班 |
83 |
b |
90 |
|
3班 |
a |
80 |
80 |
根据以上信息回答下列问题:
-
(1) 请直接写出分析数据表格中a,b的值.
-
(2) 比较这三组样本数据的平均数、中位数、众数,你认为哪个班的成绩比较好?请说明理由.
-
(3) 学校将给竞赛成绩100分的同学颁发奖状,该校七年级学生共570人,试估计需要准备多少张奖状.
 , 3,7,它的平均数为4,这组数据的中位数是.
, 3,7,它的平均数为4,这组数据的中位数是.
- 下列词语中加点的字,读音全都不相同的一组
- 下列各组物质的溶液混合后,不能发生反应的
- 已知函数则 .
- __________the news,he said nothing and went away. A.After
- —Excuse me, _____ is Zhongshan Park from here? —It’s a
- .质量是100 g的物体可能是 A.一把椅子
- 一个带电粒子从A点射入水平方向的匀强电场
- 近年来大量出现右图这样的公益广告。导致这
- .已知椭圆C:,(a>b>0)的左、右顶点分
- 右图是细胞部分膜结构的示意图,下列相关叙
- 在R上定义运算:,若不等式对任意的实数都
- 甲、乙两辆汽车沿同一路线赶赴距出发地480km
- 39、有学者提出,中国在宋代至清代的历史进
- 下图是实验室常用的仪器。 (1)图甲中仪器
- 如果你是美国公民,你投票赞成华盛顿为美国
- 单项式的系数和次数的和是 .
- 物质制备过程中离不开物质的提纯。以下除杂
- Don’t forget to wash your hands _________ you have meals
- 已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、
- 对某商店一个月内每天的顾客人数进行了统计



