八年级(初二)数学试题
一名射击运动员在某次训练中连续打靶8次,命中的环数分别是7,8,9,9,10,10,8,8,这组数据的众数与中位数分别为( )
A . 9与8
B . 8与9
C . 8与8.5
D . 8.5与9
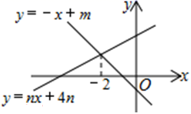
如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的解集为.
一个直角三角形两直角边的长分别为3和4,则斜边长是( )
A . 5
B . 5或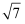 C .
C . 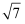 D .
D . 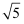
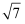 C .
C . 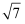 D .
D . 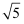
如图,在等腰直角三角形ABC中, 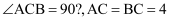 D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且 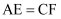 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使 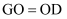 ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF
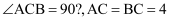 D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且 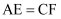 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使 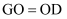 ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF 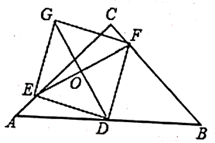
-
(1) 求证:四边形EDFG是正方形;
-
(2) 直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
如图
-
(1) 【问题探究】
如图①,锐角△ABC中,分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD , 使AE=AB , AD=AC , ∠BAE=∠CAD=90°,连接BD , CE , 试猜想BD与CE的大小关系,不需要证明.
-
(2) 【深入探究】
如图②,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD , 使AE=AB , AD=AC , ∠BAE=∠CAD , 连接BD、CE , 试猜想BD与CE的大小关系,并说明理由.
-
(3) 【拓展应用】
如图③,在△ABC中,∠ACB=45°,以AB为直角边,A为直角顶点向外作等腰直角△ABD , 连接CD , 若AC=
 ,BC=3,则CD长为.
,BC=3,则CD长为.
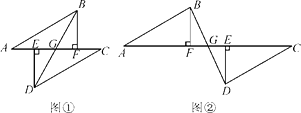
如图①,点A,E,F,C在同一直线上,AE=CF,过点E,F分别作ED⊥AC,FB⊥AC,AB=CD.
-
(1) 若BD与EF交于点G,试证明BD平分EF;
-
(2) 若将△DEC沿AC方向移动到图②的位置,其他条件不变,上述结论是否仍然成立?请说明理由.
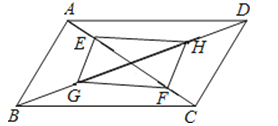
如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG.求证:GF∥HE.
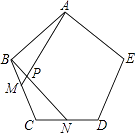
如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
-
(1) 求证:△ABM≌△BCN;
-
(2) 求∠APN的度数.
已知函数y=  x﹣1,如果函数值y>2,那么相应的自变量x的取值范围是.
x﹣1,如果函数值y>2,那么相应的自变量x的取值范围是.
 x﹣1,如果函数值y>2,那么相应的自变量x的取值范围是.
x﹣1,如果函数值y>2,那么相应的自变量x的取值范围是.
△ABC中,①若AB=BC=CA,则△ABC是等边三角形;②属于轴对称图形,且有一个角为60°的三角形是等边三角形;③有三条对称轴的三角形是等边三角形;④有两个角是60°的三角形是等边三角形,上述结论中正确的有( )
A . 1个
B . 2个
C . 3个
D . 4个
如图,经过矩形对称中心的任意一条直线把矩形分成面积分别为S1和S2的两部分,则S1与S2的大小关系是( )
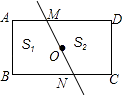
A . S1<S2
B . S1>S2
C . S1=S2
D . S1与S2的关系由直线的位置而定
要使式子  有意义,则m的取值范围是( )
有意义,则m的取值范围是( )
 有意义,则m的取值范围是( )
有意义,则m的取值范围是( )
A . m≥﹣2,且m≠2
B . m≠2
C . m≥﹣2
D . m≥2
如图,已知菱形OABC的顶点O(0,0),B(﹣2,﹣2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
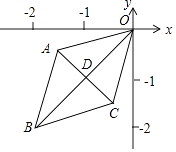
A . (1,﹣1)
B . (﹣1,﹣1)
C . (1,1)
D . (﹣1,1)
《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行.问:人与车各多少?设有  辆车,人数为
辆车,人数为  ,根据题意可列方程组为( )
,根据题意可列方程组为( )
 辆车,人数为
辆车,人数为  ,根据题意可列方程组为( )
,根据题意可列方程组为( )
A . 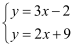 B .
B . 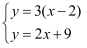 C .
C . 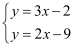 D .
D . 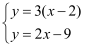
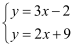 B .
B . 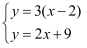 C .
C . 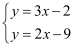 D .
D . 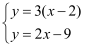
如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN。若AB=5,BC=8,则MN=。
当三角形中一个内角  是另外一个内角
是另外一个内角  的
的  时,我们称此三角形为“友好三角形”,
时,我们称此三角形为“友好三角形”,  为友好角.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角
为友好角.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角  ”的度数为.
”的度数为.
 是另外一个内角
是另外一个内角  的
的  时,我们称此三角形为“友好三角形”,
时,我们称此三角形为“友好三角形”,  为友好角.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角
为友好角.如果一个“友好三角形”中有一个内角为54°,那么这个“友好三角形”的“友好角  ”的度数为.
”的度数为.
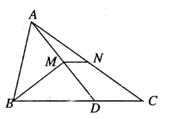
在 中,D,E分别是
中,D,E分别是 、
、 上的点,过点D作
上的点,过点D作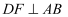 ,
, 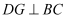 , 垂足分别是点F,G,连接
, 垂足分别是点F,G,连接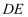 , 若
, 若 ,
, 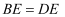 , 则下面三个结论:①
, 则下面三个结论:①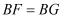 ;②
;②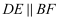 ;③
;③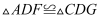 . 其中正确的是( )
. 其中正确的是( )
 中,D,E分别是
中,D,E分别是 、
、 上的点,过点D作
上的点,过点D作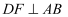 ,
, 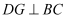 , 垂足分别是点F,G,连接
, 垂足分别是点F,G,连接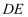 , 若
, 若 ,
, 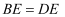 , 则下面三个结论:①
, 则下面三个结论:①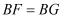 ;②
;②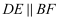 ;③
;③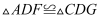 . 其中正确的是( )
. 其中正确的是( )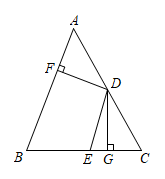
A . ①③
B . ②③
C . ①②
D . ①②③
下列运算正确的是( )
A .  B .
B . 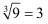 C .
C . 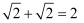 D .
D . 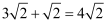
 B .
B . 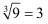 C .
C . 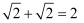 D .
D . 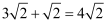
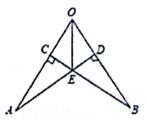
如图,已知OE平分∠AOB,BC⊥OA于点C,AD⊥OB于点D,求证:EA=EB.
如图,C、D是线段AB上两点,且AC=BD=  AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点. 在点P从点C移动到点D时,点M运动的路径长度为.
AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点. 在点P从点C移动到点D时,点M运动的路径长度为.
 AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点. 在点P从点C移动到点D时,点M运动的路径长度为.
AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点. 在点P从点C移动到点D时,点M运动的路径长度为. 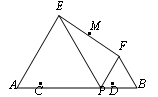
最近更新
- 某化学兴趣小组的学生,发现金属R不在初中
- 若某动物细胞内有两对同源染色体,分别用A
- 秦统一六国的最主要的主观因素是 A.秦国的商
- (08湖南怀化)“墙角数枝梅,凌寒独自开,
- You can’t imagine when they rec
- (10)用数字0,1,2,3,4,5可以组成没有重
- 现有烃的含氧衍生物A,还原A时形成醇B,氧化
- 已知定义域为R的函数是奇函数. (Ⅰ)求a,
- 类推可以实现知识迁移,但不符合事实的类推
- 下列关于明朝内阁与英国内阁相同点的比较,
- 如图,,,,则的度数为__________.
- 下列表格中的言论客观反映了当时不同政治派
- 下列各句中没有语病的一句是( ) A
- 阅读下列材料,回答相关问题。 蜜蜂“
- 某一实验小组的同学,欲通过制备固定化酵母
- _____ of this week, I will fly to Shanghai. A. By the
- It’s amazing how one dollar can change the culture of a s
- 李后主说 “问君能有几多愁,恰似一江春水
- 下图是某兴趣小组设计的一恒温箱的原理图。
- 下列实验操作中错误的是A.用规格为10ml的量筒



