八年级(初二)数学试题
分式 与下列分式相等的是( )
与下列分式相等的是( )
 与下列分式相等的是( )
与下列分式相等的是( )
A .  B .
B .  C .
C .  D . -
D . -
 B .
B .  C .
C .  D . -
D . -
22•(﹣2)3=;(  )0×3﹣2=;(﹣0.25)2013×42014=.
)0×3﹣2=;(﹣0.25)2013×42014=.
 )0×3﹣2=;(﹣0.25)2013×42014=.
)0×3﹣2=;(﹣0.25)2013×42014=.
CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.

解:∵CD是线段AB的垂直平分线(已知),
∴AC=,=BD()
在△ADC和中,
=BC,
AD=,
CD=,
∴≌().
∴∠CAD=∠CBD (全等三角形的对应角相等).
下列运算正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
计算:
-
(1) (2x3y)2•(﹣2xy)+(﹣2x3y)3÷(2x2)
-
(2) (6m2n﹣6m2n2﹣3m2)÷(﹣3m2)
-
(3) 先化简,再求值:2(x+1)2﹣5(x+1)(x﹣1)+3(x﹣1)2 , 其中x=(
 )﹣1 .
)﹣1 .
等腰三角形的一个内角是80°,则它的另外两个角的度数是( )
A . 80°、20°
B . 50°、50°
C . 80°、50°
D . 80°、20°或50°、50°
如图,在 中,AE的垂直平分线MN交BE于点C,连接AC.若
中,AE的垂直平分线MN交BE于点C,连接AC.若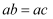 ,
,  ,
,  , 则
, 则 的周长等于( )
的周长等于( )
 中,AE的垂直平分线MN交BE于点C,连接AC.若
中,AE的垂直平分线MN交BE于点C,连接AC.若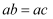 ,
,  ,
,  , 则
, 则 的周长等于( )
的周长等于( )
A . 11
B . 16
C . 17
D . 18
如图,菱形 的边长为2,
的边长为2, , 则点D的坐标为( )
, 则点D的坐标为( )
 的边长为2,
的边长为2, , 则点D的坐标为( )
, 则点D的坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在正方形ABCD中,AB=4,E,F分别是边BC,CD边上的动点,且AE=AF,设△AEF的面积为y,EC的长为x.

-
(1) 求y与x之间的函数表达式,并写出自变量x的取值范围.
-
(2) 当x取何值时,△AEF的面积最大,最大面积是多少?
-
(3) 在直角坐标系中画出y关于x的函数的图象.
受新冠肺炎疫情的影响,运城市某化工厂从2020年1月开始产量下降.借此机会,为了贯彻“发展循环经济,提高工厂效益”的绿色发展理念;管理人员对生产线进行为期5个月的升级改造,改造期间的月利润与时间成反比例函数;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2020年1月为第1个月,第  个月的利润为
个月的利润为  万元,其图象如图所示,试解决下列问题:
万元,其图象如图所示,试解决下列问题:
 个月的利润为
个月的利润为  万元,其图象如图所示,试解决下列问题:
万元,其图象如图所示,试解决下列问题: 
-
(1) 分别写出该化工厂对生产线进行升级改造前后,
 与
与  的函数表达式.
的函数表达式.
-
(2) 到第几个月时,该化工厂月利润才能再次达到100万元?
-
(3) 当月利润少于50万元时,为该化工厂的资金紧张期,问该化工厂资金紧张期共有几个月?
如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到
△EFG

-
(1) 在图中画出点P和△EFG,保留画图痕迹,简要说明理由
-
(2) 若AO=3
 ,CD=2
,CD=2  ,求A点运动到E点路径的长.
,求A点运动到E点路径的长.
化简:  ,圆圆的解答如下:
,圆圆的解答如下: 
 ,圆圆的解答正确吗?如果不正确,写出正确的解答,并求出当
,圆圆的解答正确吗?如果不正确,写出正确的解答,并求出当  时,代数式的值.
时,代数式的值.
 ,圆圆的解答如下:
,圆圆的解答如下: 
 ,圆圆的解答正确吗?如果不正确,写出正确的解答,并求出当
,圆圆的解答正确吗?如果不正确,写出正确的解答,并求出当  时,代数式的值.
时,代数式的值.
已知直线y=-x+5交x轴于A,交y轴于B,直线y=2x﹣4与x轴于D,与直线AB相交于点C.

-
(1) 求点C的坐标;
-
(2) 求四边形BODC的面积.
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.求证:

-
(1) FC=AD;
-
(2) AB=BC+AD.
计算:
-
(1)

-
(2)

下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(环) | 9.5 | 9.5 | 9.5 | 9.5 |
| 方差 | 8.5 | 7.3 | 8.8 | 7.7 |
根据表中数据,要从中选择一名成绩发挥稳定的运动员参加比赛,应选择( )
A . 甲
B . 乙
C . 丙
D . 丁
如图,在平面直角坐标系中,ABCO为平行四边形,O(0,0),A(3,1),B(1,2),反比例函数  的图象经过
的图象经过  OABC的顶点C,则k=.
OABC的顶点C,则k=.
 的图象经过
的图象经过 
已知函数  是一次函数,求m的值.
是一次函数,求m的值.
 是一次函数,求m的值.
是一次函数,求m的值.
先化简(1﹣  )÷
)÷  ,然后从不等式2x﹣6<0的非负整数解中选取一个合适的解代入求值.
,然后从不等式2x﹣6<0的非负整数解中选取一个合适的解代入求值.
 )÷
)÷  ,然后从不等式2x﹣6<0的非负整数解中选取一个合适的解代入求值.
,然后从不等式2x﹣6<0的非负整数解中选取一个合适的解代入求值.
如图,在平面直角坐标系中,菱形ABCD的顶点A(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上,若抛物线y=-x2-5x+c经过点B、C,则菱形ABCD的面积为( )

A . 15
B . 20
C . 25
D . 30
最近更新
- 下列各反应中,氧化反应与还原反应在同种元
- 玉米、甘薯是高产农作物,自引入中国来,中
- 搬开庭院中的石块,鼠妇很快就爬走了。这时
- 一射击运动员一次射击练习的成绩是(单位:
- 一定温度下,反应2SO2+O22SO3达到平衡时,n(SO2
- 已知同温同压下,下列反应的焓变和平衡常数
- 位于长江中上游的某茶场,茶园面积600亩,每年
- 魏玛共和国被称为“一个没有共和主义者的共
- 下列句子中,加线的词语使用错误的一句是(
- 地球上海洋与陆地面积之比约是 A.2:8
- 一个口袋中放着若干个红球和白球,这两种球
- 对环境污染最严重的是( ) A.生活垃圾
- When we think of leadership, we often think of strength and
- 下图为30°N纬线上某地地形剖面图,读图完成
- 已知P、A、B、C是以O为球心的球面上的四个点
- 阅读下面的文字,完成后面小题。 尼罗河谷
- 下列四个角中,最有可能与角互补的角是(
- 读世界森林面积正在逐渐消失图,回答各题。
- 胆固醇、苯、尿素进入细胞内的方式是( ) A.
- 下列关于生物圈的说法正确的是( )A.大气



