八年级(初二)数学试题
计算下列各题
-
(1) 计算:(﹣1)3﹣(
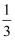 )﹣2×
)﹣2× 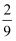 +6×|﹣
+6×|﹣ 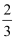 |
|
-
(2) 化简并求值:(
 )÷
)÷  ,其中a=1,b=2.
,其中a=1,b=2.
如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在何处.(不写作法,保留作图痕迹)

如图,在四边形ABCD中,AD∥BC,∠B=38°,∠C=71°.求证:AB+AD=BC.

草莓是一种极具营养价值的水果,当下正是草莓的销售旺季.某水果店以2850元购进两种不同品种的盒装草莓,若按标价出售可获毛利润1500元(毛利润=售价-进价),这两种盒装草莓的进价、标价如下表所示:
|
价格/品种 |
A品种 |
B品种 |
|
进价(元/盒) |
45 |
60 |
|
标价(元/盒) |
70 |
90 |
-
(1) 求这两个品种的草莓各购进多少盒;
-
(2) 该店计划下周购进这两种品种的草莓共100盒(每种品种至少进1盒),并在两天内将所进草莓全部销售完毕(损耗忽略不计).因B品种草莓的销售情况较好,水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒.如何安排进货,才能使毛利润最大,最大毛利润是多少?
为加强公路的节水意识,合理利用水资源,某市对居民用水实行阶梯水价,居民家庭每月用水量划分为两个阶梯,一、二阶梯用水的单价之比等于1:2,如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系,其中射线AB表示第二级阶梯时y与x之间的函数关系.

-
(1) 写出点B的实际意义;
-
(2) 求射线AB所在直线的表达式.
化简: 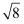 ﹣
﹣  =.
=.
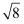 ﹣
﹣  =.
=.
如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的的长度为.

已知x2-y2=6,且x=2-y,则x-y=.
已知一组数据1,2,0,-1,x,1的平均数是1,那么这组数据的方差是.
多项式mx2-m与多项式x2-2x+1的公因式是( )
A . x-1
B . x+1
C . x2-1
D . (x-1)2
分解因式:
-
(1) 3a3﹣6a2+3a.
-
(2) a2(x﹣y)+b2(y﹣x).
已知在△ABC中,∠C=90°,AB=4,AC=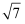 .
.
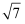 .
.

-
(1) 求BC;
-
(2) 求sinA.
将一副三角板按图中的方式叠放,则∠α等于( )

A . 75°
B . 60°
C . 45°
D . 30°
先化简,再求值:  ,其中
,其中  .
.
 ,其中
,其中  .
.
如图,等边△ABC的边长是6,则高AD=( )

A . 3
B .  C .
C . 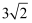 D .
D . 
 C .
C . 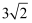 D .
D . 
如图,在正方形  中,E为
中,E为  边上一点,F为
边上一点,F为  延长线上一点,且
延长线上一点,且  ,连接
,连接  .给出下列至个结论:①
.给出下列至个结论:①  ;②
;②  ;③
;③  ;④
;④  ;⑤
;⑤  .其中正确结论的个数是( )
.其中正确结论的个数是( )
 中,E为
中,E为  边上一点,F为
边上一点,F为  延长线上一点,且
延长线上一点,且  ,连接
,连接  .给出下列至个结论:①
.给出下列至个结论:①  ;②
;②  ;③
;③  ;④
;④  ;⑤
;⑤  .其中正确结论的个数是( )
.其中正确结论的个数是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
分解因式:  .
.
 .
.
下列各式计算正确的是( )
A . 8  ﹣2
﹣2  =6
B . 5
=6
B . 5  +5
+5  =10
=10  C . 4
C . 4  ÷2
÷2  =2
=2  D . 4
D . 4  ×2
×2  =8
=8 
 ﹣2
﹣2  =6
B . 5
=6
B . 5  +5
+5  =10
=10  C . 4
C . 4  ÷2
÷2  =2
=2  D . 4
D . 4  ×2
×2  =8
=8 
已知反比例函数  和一次函数y=2x+b,其中一次函数的图象经过点A(﹣1,﹣3)和B(1,m).反比例函数图象经过点B.
和一次函数y=2x+b,其中一次函数的图象经过点A(﹣1,﹣3)和B(1,m).反比例函数图象经过点B.
 和一次函数y=2x+b,其中一次函数的图象经过点A(﹣1,﹣3)和B(1,m).反比例函数图象经过点B.
和一次函数y=2x+b,其中一次函数的图象经过点A(﹣1,﹣3)和B(1,m).反比例函数图象经过点B. 
-
(1) 求反比例函数的解析式和一次函数的解析式;
-
(2) 若直线
 交x轴于C,交y轴于D,点P为反比例函数
交x轴于C,交y轴于D,点P为反比例函数  (x>0)的图象上一点,过P作y轴的平行线交直线CD于E,过P作x轴的平行线交直线CD于F,
(x>0)的图象上一点,过P作y轴的平行线交直线CD于E,过P作x轴的平行线交直线CD于F, ①请问:在该反比例函数图象上是否存在点P,使△PFE≌△OCD?若存在,求点P的坐标;若不存在,请说明理由.
②求证:DE•CF为定值.
下列图象中,y不是x的函数的是 



A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新
- 2009年1月西藏自治区九届人大二次会议通过决
- 若函数y=f(x)是函数y=ax(a>0,且a≠1)的反函
- Can you imagine the singer _____ so much in public? A. being
- 关于原子的组成,下列说法正确的是
- 下述实验设计或操作正确的是( ) 选项实验
- 村庄的语言 许锋 (1)很多人一生都在做一件
- “蒸汽时代”和“电气时代”的来临都 ①推
- 下列关于明清商品经济的叙述,错误的是 …()
- 下列有关事实不能用金属活动性顺序解释的是
- 下列说法中,正确的个数为() ①角是轴对
- 已知氧元素的结构示意图为: 下
- 下列各组溶液不加其它试剂就能鉴别的是 A.N
- 当前一些地方封建迷信活动沉渣泛起,如占卦
- 点A(,5),B(, )关于轴对称,则.
- 三个数,G,成等比数列. 且>0,则 .
- 右面是一幅“中医”为当前国际金融危机下全
- 人人是学习之人,时时是学习之时。建立全民
- 下列有关命题的说法正确的是( )A.命题“
- 在“验证力的平行四边形定则”的实验中,采
- 下列物质化学式的读法和写法都正确的是( �



