八年级(初二)数学试题
已知:如图,等边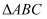 中,点D、E分别在
中,点D、E分别在 、
、 边上,且
边上,且 ,
,  、
、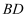 相交于点O,连接
相交于点O,连接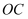 .
.
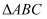 中,点D、E分别在
中,点D、E分别在 、
、 边上,且
边上,且 ,
,  、
、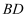 相交于点O,连接
相交于点O,连接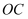 .
. 
-
(1) 如图1,当
 时,
时, 的度数为 ;
的度数为 ;
-
(2) 如图2,当
 时,
时,①求
 的值;
的值;②求证:
 .
.
如图,AC为矩形ABCD的对角线,DE⊥AC于E,BF⊥AC于F。
求证:DE=BF

叫做因式分解.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为12米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).

-
(1) 如何才能围成矩形花园的面积为75m2?
-
(2) 能够围成面积为101m2的矩形花园吗?如能说明围法,如不能,说明理由.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.

-
(1) 若ED⊥EF,求证:ED=EF;
-
(2) 在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);
-
(3) 若ED=EF,ED与EF垂直吗?若垂直给出证明.
把边长为 6 厘米的正方形 ABCD 沿对角线 AC 截成两个直角三角形,在两个三角形内按下图剪下两个内接正方形Ⅰ、Ⅱ,这两个正方形的面积比较( )

A . Ⅰ大
B . Ⅱ大
C . 一样大
D . 无法确定谁大
计算: 

若xy>0,则  的值为.
的值为.
 的值为.
的值为.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为.

下列函数中,是一次函数的有( )
⑴y=x2-1 (2)y=2x-1 (3)y=  (4)y=-3x
(4)y=-3x
A . 4个
B . 3个
C . 2个
D . 1个
如图,一次函数的y=kx+b图象经过A(2,4)、B(0,2)两点,与x轴交于点C,则ΔAOC的面积为.

如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点.如果两个正方形的边长都等于2,那么正方形A′B′C′OA绕O点无论怎样转动,两个正方形重叠的部分的面积是.

计算(-a3)2的结果是( )
A . -a5
B . a5
C . a6
D . -a6
把一副常用的三角板如图所示拼在一起,那么图中∠ABC=

已知
 ,那么
,那么
 的值是( )
的值是( )
 ,那么
,那么
 的值是( )
的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
水源村在今年退耕还林活动中,计划植树200亩,全村在完成植树40亩后,某环保组织加入村民植树活动,并且该环保组织植树的速度是全村植树速度的1.5倍,整个植树过程共用了13天完成.
-
(1) 全村每天植树多少亩?
-
(2) 如果全村植树每天需2000元工钱,环保组织是义务植树,因此实际工钱比计划节约多少元?
能够将一个三角形的面积平分的线段是( )
A . 一边上的高线
B . 一个内角的角平分线
C . 一边上的中线
D . 一边上的中垂线
如图,直线y=ax+b过点A(0,3)和点B(-7,0),则方程ax+b=0的解是( )

A . x=0
B . x=3
C . x=-7
D . x=-4
如图,在正方形ABCD中,点E是AB边上的一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与GB交于点N,连接CG.

-
(1) 求证:CD⊥CG;
-
(2) 若tan∠MEN=
 ,求
,求  的值;
的值;
-
(3) 已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为
 ?请说明理由.
?请说明理由.
等腰三角形的两边长分别是2,4,则它的周长是( )
A . 8
B . 10
C . 8或10
D . 9
最近更新
- 如图是甲、乙两射击运动员的10次射击训练成
- ,芳草萋萋
- 【2013年·内蒙古省包头市】 【试题】6.按要
- (坐标系与参数方程选做题) 若直线(t为参
- 紫杉醇是一种新型抗癌药,其分子式为C47H51NO1
- 2010年3月,全国政协第十一届三次会议和全国
- 已知圆锥的母线长是5cm,侧面积是15πcm2,则
- 常见金属R与硝酸银溶液反应的化学方程式为R+
- 根据短文内容,从短文后的选项中选出能填入
- 小华想知道学校旗杆的高度,他发现旗杆上的
- 设等差数列的前项和为,若,则 A7 �
- --When shall we meet again next week? ---_____ day is possi
- 20.仿照下面的例句,另选两个话题,各写一
- 2009年是新世纪以来我国经济发展最为困难的
- 若是偶函数,且当的解集是 �
- 函数的定义域是() A.[2,3)
- 小明想知道牛奶的密度,在实验室进行了下面
- 马克思主义中国化,就是将马克思主义的基本
- 实验室中一般采用高锰酸钾或氯酸钾的受热分
- 作文(60分) 在成长过程中,你所走的



