八年级(初二)数学试题
如图,△ABC中,∠C=90°,点D在线段BC上,连接AD,若∠CAD=  ∠B,AB=8,CD=2,则AD的长为.
∠B,AB=8,CD=2,则AD的长为.
 ∠B,AB=8,CD=2,则AD的长为.
∠B,AB=8,CD=2,则AD的长为. 
如图,△ABC中,∠ACB=90°,点D是边BC上一点,DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.

-
(1) 求证:EF=CF;
-
(2) 若∠BAC=30°,连接EC,试判断△EFC 的形状,并说明理由.
某校在“校园十佳歌手”比赛上,六位评委给1号选手的评分如下:90,96,91,96,95,94.那么,这组数据的众数和中位数分别是( )
A . 96,94.5
B . 96,95
C . 95,94.5
D . 95,95
如图1,在矩形MNPO中,动点R从点N出发,沿N→P→O→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPO的周长是( )

A . 11
B . 15
C . 16
D . 24
若最简二次根式 与
与 可以合并,则
可以合并,则 .
.
 与
与 可以合并,则
可以合并,则 .
.
下列因式分解错误的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如果等腰三角形的两边长分别为4和7,则三角形的周长为 .
如图,AD是∆ABC中∠BAC的平分线,DE⊥AB于点E,  ,DE=2,AB=4,则AC的长是( )
,DE=2,AB=4,则AC的长是( )
 ,DE=2,AB=4,则AC的长是( )
,DE=2,AB=4,则AC的长是( ) 
A . 3
B . 4
C . 5
D . 6
如图,  ,
, 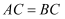 ,
,  ,
,  ,垂足分别是点
,垂足分别是点  、
、  ,
,  ,
,  ,则
,则  的长是( )
的长是( )
 ,
, 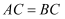 ,
,  ,
,  ,垂足分别是点
,垂足分别是点  、
、  ,
,  ,
,  ,则
,则  的长是( )
的长是( ) 
A .  B . 2
C . 4
D . 6
B . 2
C . 4
D . 6
 B . 2
C . 4
D . 6
B . 2
C . 4
D . 6
如果小明想清楚表达自己从上初中以来到本学期期末6次大型考试中数学成绩的变化情况,最好选用( )
A . 扇形图
B . 折线图
C . 复合条形图
D . 频数直方图
在雨地里放置一个无盖的容器,如果雨水均匀地落入容器,容器内水面高度  与时间
与时间  的函数图象如图所示,那么这个容器的形状可能是( )
的函数图象如图所示,那么这个容器的形状可能是( )
 与时间
与时间  的函数图象如图所示,那么这个容器的形状可能是( )
的函数图象如图所示,那么这个容器的形状可能是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  D .
D . 
如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:

①∠EBC=∠C;②△EAF∽△EBA;③BF=3EF;④∠DEF=∠DAE,其中结论正确的个数有( )
A . 1个
B . 2个
C . 3个
D . 4个
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
①用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
②用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
③用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
④用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
|
n |
3 |
4 |
5 |
6 |
|
m |
1 |
0 |
1 |
1 |
探究二:
-
(1) 用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(仿照上述探究方法,写出解答过程,并把结果填在表②中)
-
(2) 分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)
n
7
8
9
10
m
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
-
(3) 解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
n
4k﹣1
4k
4k+1
4k+2
m
-
(4) 问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了根木棒.(只填结果)
下列式子由左到右的变形中,属于因式分解的是( )
A . (x+2y)2=x2+4xy+4y2
B . x2-2y+4=(x-1)2
C . 3x2-2x-1=(3x+1)(x-1)
D . m(a+b+c)=ma+mb+mc
如图,△ABC是等边三角形,AD是BC边上的中线,点E在AC上,且∠CDE=20°,现将△CDE沿直线DE折叠得到△FDE,连结BF.∠BFE的度数是.

一组数据2,3,5,4,4的中位数和平均数分别是( )
A . 4和3.5
B . 4和3.6
C . 5和3.5
D . 5和3.6
如图,点A在第一象限内,其坐标为(2,1),以OA为边在x轴上方作正方形OABC,则正方形OABC的顶点C的坐标是( )

A . (﹣2,1)
B . (1,3)
C . (1,2)
D . (﹣1.2)
如图,已知△ABC≌△CDE,下列结论中不正确的是( )

A . AC=CE
B . ∠BAC=∠ECD
C . ∠ACB=∠ECD
D . ∠B=∠D
函数  的图象经过点P(-1,3),则
的图象经过点P(-1,3),则  的值为( )
的值为( )
 的图象经过点P(-1,3),则
的图象经过点P(-1,3),则  的值为( )
的值为( )
A . 3
B . -3
C .  D . -
D . - 
 D . -
D . - 
如图,∠A+∠B+∠C+∠D+∠E+∠F=.

最近更新
- 若不等式8x4+8(a-2)x2-a+5>0对于任意实数x均成立
- The enemy troop suddenly took the small village by surprise
- 分裂期细胞的细胞质中含有一种促进染色质凝
- 一个几何体的三视图如图所示,则该几何体
- “嫦娥一号”卫星完成四大科学目标之一是探
- My daughter told me that_____ of her homework had been fi
- 如图Ox、Oy、Oz为相互垂直的坐标轴,Oy轴为竖
- 2011年7月至2012年1月,黑龙江省设区的市、县(
- 在人体体细胞增殖的一个细胞周期中,在纺锤
- 在《赤壁》中, “ , 。
- 人体的发育是从下列哪项开始的( )
- 如图11 所示,小华在滑冰场上快速滑行,在10s
- 在“测定小灯泡的电功率”实验中,电源电压
- ------What did you do last weekend, Jack? ------ Well,
- Let's go to cinema that'll take your mind off
- 市场上的名牌产品,一般来说,价格都比较高
- 、我国青铜文化的灿烂时期,是以司母戊鼎为
- 1984年6月,邓小平说:“中国有香港、台
- 下列各种行为中,属于学习行为的是(
- The telephone lines were brought down by the ____



