七年级(初一)数学下学期下册试题
不等式2x+1≤3的解集在数轴上表示正确的是( )
A . 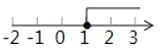 B .
B .  C .
C . 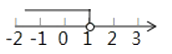 D .
D . 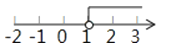
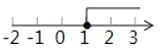 B .
B .  C .
C . 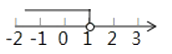 D .
D . 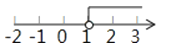
某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:
|
甲 |
乙 |
丙 |
|
|
数量(个) |
m |
3m |
n |
|
批发单价(元) |
a(1≤m≤10) |
b |
10 |
|
0.8a(m>10) |
-
(1) 当m=5时,若这三种礼器共批发35个,甲礼品的总价不低于丙礼品的总价,求a的最小值;
-
(2) 已知该店用1320元批发了这三种礼品,且a=5b:
①当m=25时,若批发这三种礼品的平均单价为11元/个,求b的值;
②当7<m<20时,若该店批发了20个丙礼品,且a为正整数,求a的值。
计算:
-
(1) (
 +
+  + 5)÷
+ 5)÷  -
- 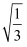 ×
× 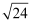 -
-  ;
;
-
(2) (-3)﹣2 +
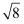 -|1-2
-|1-2  |-(
|-(  -3)0
-3)0
2018年8月31日,华为麒麟980处理器在  德国柏林国际电子消费展会中正式发布,这款处理器创造了“六个世界第一”.麒麟980是国内第一款采用台积电7
德国柏林国际电子消费展会中正式发布,这款处理器创造了“六个世界第一”.麒麟980是国内第一款采用台积电7  工艺制造而成的移动处理器.7
工艺制造而成的移动处理器.7  也就是0.000000007
也就是0.000000007 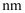 ,把0.000000007
,把0.000000007  这个数据用科学记数法表示为.
这个数据用科学记数法表示为.
 德国柏林国际电子消费展会中正式发布,这款处理器创造了“六个世界第一”.麒麟980是国内第一款采用台积电7
德国柏林国际电子消费展会中正式发布,这款处理器创造了“六个世界第一”.麒麟980是国内第一款采用台积电7 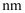 工艺制造而成的移动处理器.7
工艺制造而成的移动处理器.7 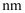 也就是0.000000007
也就是0.000000007 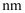 ,把0.000000007
,把0.000000007  这个数据用科学记数法表示为.
这个数据用科学记数法表示为.
某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目 (被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.

已知:如图(1),如果AB∥CD∥EF.
那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
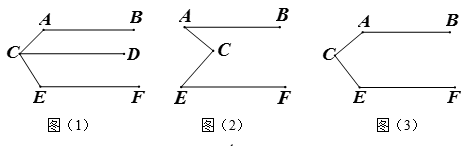

-
(1) 小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是.
-
(2) 接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系:.
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系:.
-
(3) 小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.
已知 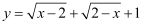 ,
, 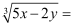 .
.
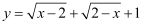 ,
, 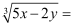 .
.
为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
|
选项 |
人数 |
频率 |
|
A |
15 |
0.3 |
|
B |
10 |
m |
|
C |
5 |
0.1 |
|
D |
n |
|
|
E |
5 |
0.1 |
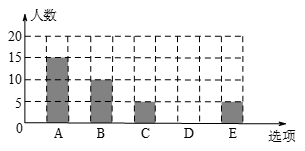
根据以上信息回答下列问题:
-
(1) 这次调查的样本容量是;
-
(2) 统计表中m=,n=,补全条形统计图;
-
(3) 若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.
机械表是日常生活中常见的一类钟表,与电子表不同,机械表受环境、机芯等因素的影响常会产生走时误差.现为了比较市场上甲、乙两款机械表的精准度,从两款表中,各随机抽取一块进行每日走时误差的检测,连续检测10天,两款表每日走时误差的统计数据如图(单位:秒):
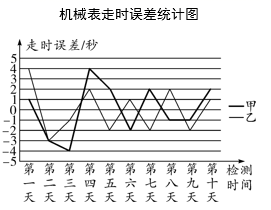
-
(1) 甲、乙两种机械表的平均走时误差分别是多少?
-
(2) 小明现计划购买一块机械表,如果仅从走时的准确度考虑,你会推荐他购买甲、乙哪一种,请说明理由.
解不等式组: 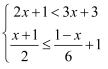 .
.
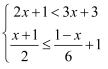 .
.
如果 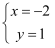 是二元一次方程mx+y=3的一个解,则m的值是( )
是二元一次方程mx+y=3的一个解,则m的值是( )
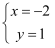 是二元一次方程mx+y=3的一个解,则m的值是( )
是二元一次方程mx+y=3的一个解,则m的值是( )
A . -2
B . 2
C . -1
D . 1
如图,将△ABC沿边BC向右平移2个单位长度得到△DEF,若AC的长为3个单位长度,则四边形ACFD的周长为( )
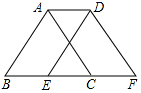
A . 6
B . 10
C . 8
D . 12
如图,Rt△ABC的直角边长分别为12和16,在其内部有n个小直角三角形,则这n个小直角三角形周长之和为.

计算: 

下列四个数中,在-2到0之间的数是( )
A . -1
B . 1
C . -3
D . 3
不等式 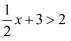 的负整数解为 .
的负整数解为 .
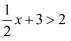 的负整数解为 .
的负整数解为 .
一方有难,八方支援.“新冠肺炎”疫情来袭,除了医务人员主动请缨走向抗疫前线,众多企业也伸出援助之手,某公司用甲、乙两种货车向武汉运送爱心物资,两次满载的运输情况如表:
甲种货车(辆) | 乙种货车(辆) | 总量(吨) | |
第一次 | 4 | 5 | 31 |
第二次 | 3 | 6 | 30 |
-
(1) 甲、乙两种货车每辆分别能装货多少吨?
-
(2) 现有45吨物资需要再次运往武汉,准备同时租用这两种货车,每辆均全部装满货物,问有哪几种租车方案?
对于二元一次方程组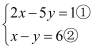 , 我们把x,y的系数和方程右边的常数分离出来组成一个矩阵:
, 我们把x,y的系数和方程右边的常数分离出来组成一个矩阵: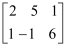 , 用加减消元法解二元一次方程组的过程,就是对方程组中各方程中未知数的系数和常数项进行变换的过程.若将②×5,则得到矩阵
, 用加减消元法解二元一次方程组的过程,就是对方程组中各方程中未知数的系数和常数项进行变换的过程.若将②×5,则得到矩阵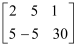 , 用加减消元法可以消去y,如解二元一次方程组
, 用加减消元法可以消去y,如解二元一次方程组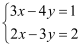 时,我们用加减消元法消去x,得到的矩阵应是( )
时,我们用加减消元法消去x,得到的矩阵应是( )
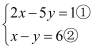 , 我们把x,y的系数和方程右边的常数分离出来组成一个矩阵:
, 我们把x,y的系数和方程右边的常数分离出来组成一个矩阵: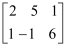 , 用加减消元法解二元一次方程组的过程,就是对方程组中各方程中未知数的系数和常数项进行变换的过程.若将②×5,则得到矩阵
, 用加减消元法解二元一次方程组的过程,就是对方程组中各方程中未知数的系数和常数项进行变换的过程.若将②×5,则得到矩阵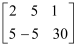 , 用加减消元法可以消去y,如解二元一次方程组
, 用加减消元法可以消去y,如解二元一次方程组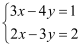 时,我们用加减消元法消去x,得到的矩阵应是( )
时,我们用加减消元法消去x,得到的矩阵应是( )
A . 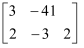 B .
B . 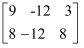 C .
C . 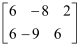 D .
D . 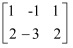
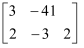 B .
B . 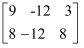 C .
C . 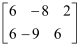 D .
D . 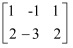
关于体育选考项目统计图
项目 | 频数 | 频率 |
A | 80 | b |
B | c | 0.3 |
C | 20 | 0.1 |
D | 40 | 0.2 |
合计 | a | 1 |
-
(1) 求出表中a,b,c的值,并将条形统计图补充完整.
表中a=,b=,c=.
-
(2) 如果有3万人参加体育选考,会有多少人选择篮球?
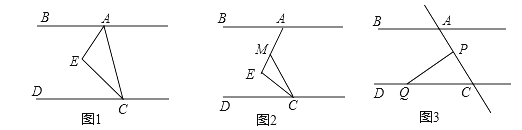
如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.
最近更新
- 北京奥运火炬手金晶9岁的时候,由于患上了恶性肿瘤,左腿进行了高位截肢,但他并没有就此消沉,而是选择了轮椅击剑作为自己奋斗
- 下列各组离子在溶液中能大量共存的是()A.酸性溶液 Na+、K+、MnO、Br- B.酸性溶液 Fe3+、NH、SCN
- (12分)随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示. (1)根据茎
- ,疏而不漏。
- 若正数a、b的等差中项为,且x=a+,y=b+,则x+y的最小值为_______________.
- 西双版纳是少数民族聚居的地方,当地喜欢孔雀舞、欢度泼水节的民族是 A、汉族 B、傣族 C、壮族
- 导电塑料的主要成分是聚乙炔,在聚乙炔中掺入某些盐,塑料就有了导电性。通常塑料是电的绝缘体,导电塑料的发现,大大激发了科学
- 世界上第一部由国家编定颁布的药典是 ( ) A.《黄帝内经》B.《唐本草》 C.《神农本草经》
- (本小题满分13分) 已知函数,其中为常数,且. (I)当时,求在( )上的值域; (II)若对任意恒成立,
- 根据下图判断2014年以来人民币兑美元汇率变动的趋势,并据此推算对我国进出口贸易产生的影响。下列选项中正确的是:A.人民
- For many seniors in some universities, the final year can be
- On the floor______ an old man, who had been killed in the fi
- 右图是电解CuCl2溶液的装置,其中c、d为石墨电极。则下列有关 的判断正确的是A.a为负极、b为正极
- 2010年12月20日,全国人大常委会开始二审的刑法修正案(八)草案,对“危险驾驶犯罪”条款进行了再次修改,进一步加大了
- 下列说法不正确的是( )A. 任何反应都伴有能量的变化B. 化学反应中的能量变化可表现为热量的变化C. 反应物的总能量
- 下列实验中,有关仪器的下端必须插入液面以下的是 ①制备乙烯时用的温度计;②制备氯气装置中的分液漏斗;③制取氨水时氨气溶于
- 材料一 2011年12月4日是第11个法制宣传日,其主题是“深入学习宣传宪法,大力弘扬法治精神”,中共中央以此为契机,
- 下列实验操作与预期目的或所得结论一致的是( ) 选项 实验操作 实验目的或结论 A 某钠盐溶液中加入盐酸酸化的硝酸钡
- 关于非洲的叙述,不正确的是( ) A 平均高度据各洲之首,被称为“高原大陆” B 热带气候面积在各洲中最大,
- 医生让肺结核患者在传染病医院治疗主要是为了 A、控制传染源 B、切断传播途径 C、保护易感人群 D、研究结



