七年级(初一)数学下学期下册试题
“千年越窑,秘色慈溪”,为了解学生对慈溪秘色瓷的熟悉度,某校设置了非常了解,基本了解,很少了解,不了解四个选项,随机抽查了部分学生进行问卷调查,要求每名学生只选其中的一项,并将抽查结果绘制成如下不完整的统计图。


根据图中信息, 解答下列问题:
-
(1) 本次接受问卷调查的学生有多少人?
-
(2) 求图2中 “很少了解” 的扇形圆心角的度数.
-
(3) 全校共有960名学生, 请你估计全校学生中“非常了解”秘色瓷的学生共有多少人?
计算: 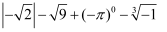
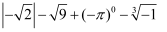
25的平方根是( )
A . 5
B . ±5
C . ±2
D . 4
32的5次方根是.
一个数的立方等于它本身,这个数是( ).
A . 0
B . 1
C . -1,1
D . -1,1,0
阅读材料:求不等式 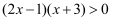 的解集
的解集
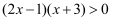 的解集
的解集
解:根据“同号两数相乘,积为正”
可得① 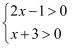 或②
或② 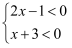
解不等式组①,得 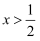 ;
;
解不等式组②,得 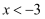
所以原不等式组的解集为 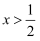 或
或 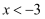 .
.
请你仿照上述方法解决下列问题:求不等式 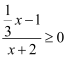 的解集.
的解集.
解不等式组:
-
(1)

-
(2)

下列四个数中,属于无理数的是( )
A .  B . -
B . -  C . 0
D .
C . 0
D . 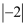
 B . -
B . -  C . 0
D .
C . 0
D . 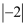
有下列各数:  ,
,  ,
, 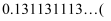 相邻两个3之间依次多一个
相邻两个3之间依次多一个 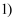 ,
, 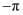 ,
,  ,
,  ,其中无理数有
,其中无理数有 

 ,
,  ,
, 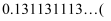 相邻两个3之间依次多一个
相邻两个3之间依次多一个 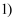 ,
, 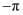 ,
,  ,
,  ,其中无理数有
,其中无理数有 

A . 1个
B . 2个
C . 3个
D . 4个
平面直角坐标系中,若P(m,n)在第三象限且到x轴,y轴的距离分别为2,3,则点P的坐标为( )
A . (-2,3)
B . (-2,-3)
C . (3,-2)
D . (-3,-2)
某细胞截面可以近似看成圆,它的半径约为0.000 000787m,则0.000 000787用科学记数法表示为( )
A . 7.87×107
B . 7.87×10﹣7
C . 0.787×10﹣7
D . 7.87×10﹣6
-
(1) 计算:|-3|+(1-
 )0-
)0-  -(-2)
-(-2)
-
(2) 化简:(a-3)2-a(a+8)
在直角坐标系中,点A在x轴上,且到原点的距离为5,则A点的坐标为;过点(3,-4)且平行于x轴的直线与y轴的交点坐标为.
阅读下列材料,解答下面的问题:我们知道方程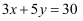 有无数个解,但在实际问题中往往只需求出其正整数解.例:由
有无数个解,但在实际问题中往往只需求出其正整数解.例:由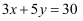 , 得
, 得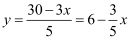 (
( 、
、 为正整数).要使
为正整数).要使 为正整数,则
为正整数,则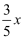 为正整数,可知
为正整数,可知 为5的倍数,从而
为5的倍数,从而 , 代入
, 代入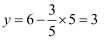 . 所以
. 所以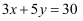 的正整数解为
的正整数解为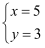 .
.
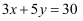 有无数个解,但在实际问题中往往只需求出其正整数解.例:由
有无数个解,但在实际问题中往往只需求出其正整数解.例:由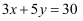 , 得
, 得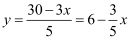 (
( 、
、 为正整数).要使
为正整数).要使 为正整数,则
为正整数,则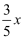 为正整数,可知
为正整数,可知 为5的倍数,从而
为5的倍数,从而 , 代入
, 代入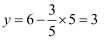 . 所以
. 所以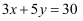 的正整数解为
的正整数解为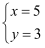 .
.
-
(1) 请你直接写出方程
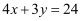 的正整数解;
的正整数解;
-
(2) 若
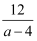 为自然数,则求出满足条件的正整数
为自然数,则求出满足条件的正整数 的值;
的值;
-
(3) 关于
 ,
,  的二元一次方程组
的二元一次方程组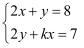 的解是正整数,求整数
的解是正整数,求整数 的值.
的值.
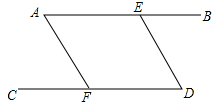
如图,AB∥CD,∠A=∠D,判断AF与ED的位置关系,并说明理由.
如图, 点为
点为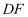 上的点,
上的点, 为
为 上的点,
上的点,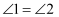 ,
, 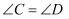 , 求证:
, 求证: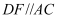 .
.
 点为
点为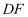 上的点,
上的点, 为
为 上的点,
上的点,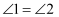 ,
, 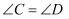 , 求证:
, 求证: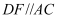 .
. 
已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: 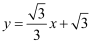 对称.
对称.
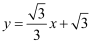 对称.
对称. 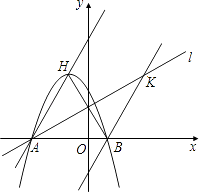
-
(1) 求A、B两点坐标,并证明点A在直线l上;
-
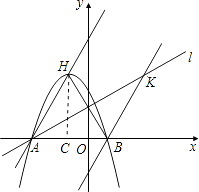
(2) 求二次函数解析式;
-
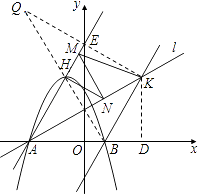
(3) 过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.
已知,在Rt△ABC中,∠ABC=90°,AB=BC=2,AD平分∠BAC,交BC于D,将△ABC沿AD折叠,B点落在AC边上的E点处,求△CDE的周长.

在解二元一次方程组时,我们的基本思路是“消元”,即通过“代入法”或“加减法”将“二元”化为“一元”,这个过程体现的数学思想是( )
A . 数形结合思想
B . 转化思想
C . 分类讨论思想
D . 类比思想
下列说法正确的是( )
A .  的系数是5
B .
的系数是5
B . 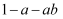 是二次三项式
C .
是二次三项式
C .  是6次单项式
D . 将1.804四舍五入精确到0.01的结果为1.8
是6次单项式
D . 将1.804四舍五入精确到0.01的结果为1.8
 的系数是5
B .
的系数是5
B . 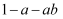 是二次三项式
C .
是二次三项式
C .  是6次单项式
D . 将1.804四舍五入精确到0.01的结果为1.8
是6次单项式
D . 将1.804四舍五入精确到0.01的结果为1.8
最近更新
- 6.下列四项能正确表示基因分离定律实质的是
- (08年大连市一模理) 设复数等于 �
- (2007年全国卷Ⅱ高考题)右图纵向表示海洋不
- 现代使用的下列材料中,不属于碳纤维复合材
- 下列说法正确的是( ) A.pH=2与pH=1
- 物质检验时,首先对试样进行外观观察,试样
- 如图,AD是△ABC的角平分线,DE∥CA,交AB于点E
- 配制100 mL 1 mol·L-1氢氧化钠溶液,下列操作
- 我国拥有较丰富的地热资源,其开发利用前景
- 如图所示,在绳下端挂一物体,用力F拉物体
- 质量分别为mA=0.2kg,mB=0.4 kg的两滑块A、B由
- 工业革命中,在动力的发明和使用上,具有开
- 已知集合P={平面直角坐标系下直线的倾斜角}
- 生活离不开化学,请用相关序号填空:A.纯
- 已知,则的大小关系是( ) A.
- (09年湛江二中月考)(17分)在绝缘水平面上,
- 下列计算正确的是( ). A. x4·x4=x16 B. (a3)2·a4=a
- The winter comes, it is ________ snow everywhere, and the bi
- 写出同时具备下列两个条件的一次函数(正比
- 如图5所示,直线A为电源口的路端电压与电流



