七年级(初一)数学下学期下册试题
解不等式组: 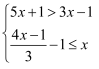
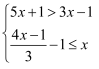
从1、2、3三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列各数: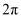 ,
, 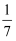 , 0,
, 0,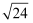 , 0.333333,
, 0.333333, ,
, 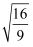 , 3.14,
, 3.14,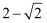 中,无理数有( )
中,无理数有( )
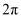 ,
, 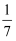 , 0,
, 0,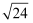 , 0.333333,
, 0.333333, ,
, 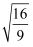 , 3.14,
, 3.14,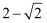 中,无理数有( )
中,无理数有( )
A . 3个
B . 4个
C . 5个
D . 6个
如图的三张卡片除正面图案外完全相同,分别印有杭州2022年第19届亚运会的吉祥物—宸宸、琮琮和莲莲.现将三张卡片背面朝上放置,打乱后随机抽取一张,恰好抽到“莲莲”的概率是( )

A . 1
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
把下列各数填入相应的集合中:
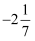 ,0,7,-0.08,-53,3.14,+22,
,0,7,-0.08,-53,3.14,+22,  .
.
正整数集合:{ …}
分数集合:{ …}
负有理数集合:{ …}
若 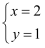 是关于x,y的方程ax- y=3的解,则a的值是( )
是关于x,y的方程ax- y=3的解,则a的值是( )
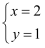 是关于x,y的方程ax- y=3的解,则a的值是( )
是关于x,y的方程ax- y=3的解,则a的值是( )
A . 1
B . 2
C . 3
D . 4
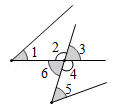
如图,下列推理及所注明的理由都正确的是: ( )
A . 因为DE∥BC,所以∠1=∠C(同位角相等,两直线平行)
B . 因为∠2=∠3,所以DE∥BC(两直线平行,内错角相等)
C . 因为∠1=∠C,所以DE∥BC(两直线平行,同位角相等)
D . 因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等)
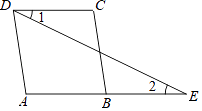
如图,已知AD∥BC,∠1=∠2,试说明∠A=∠C.
如图,下列结论中错误的是( )

A .  与
与  是同旁内角
B .
是同旁内角
B .  与
与  是内错角
C .
是内错角
C .  与
与 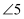 是内错角
D .
是内错角
D . 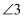 与
与 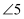 是同位角
是同位角
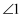 与
与  是同旁内角
B .
是同旁内角
B . 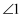 与
与 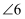 是内错角
C .
是内错角
C .  与
与 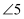 是内错角
D .
是内错角
D . 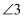 与
与  是同位角
是同位角
 的绝对值是,
的绝对值是,  的平方根是.
的平方根是.
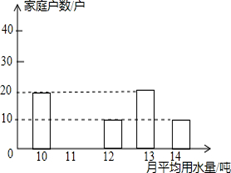
为了倡导“节约用水,从我做起”,市政府决定对某小区500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.
-
(1) 请将条形统计图补充完整;
-
(2) 求这100个样本数据的平均数,众数和中位数。
-
(3) 根据样本数据,估计该小区500户家庭中月平均用水量超过12吨的约有多少户?
已知点A在x轴上方,y轴左侧,到x轴的距离是3,到y轴的距离是4,那么点A的坐标是.
如图,将一张正方形纸片经两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是图中的哪一个( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,P是直线l外一点,A、B、C、D在直线l上,则PA、PB、PC、PD四条线段中最短的线段是.

如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=,阴影部分面积为.
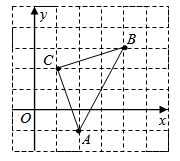
如图,平面直角坐标系中,  的顶点都在网格点上,其中
的顶点都在网格点上,其中  点坐标为
点坐标为 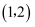 .
.
 的顶点都在网格点上,其中
的顶点都在网格点上,其中  点坐标为
点坐标为 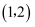 .
. 
-
(1) 写出点
 ,
,  的坐标:
的坐标:  (,),
(,),  (,)
(,)
-
(2) 将
 先向左平移2个单位长度,再向上平移1个单位长度,得到
先向左平移2个单位长度,再向上平移1个单位长度,得到  ,则
,则  的三个顶点坐标分别是
的三个顶点坐标分别是 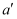 (,),
(,), 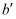 ( ,),
( ,), 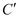 ( ,)
( ,)
-
(3) 平移
 到
到 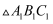 ,
,  点的对应点
点的对应点 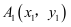 ,
,  点对应点
点对应点  ,且
,且 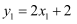 ,
,  ,请直接写出
,请直接写出  的坐标.
的坐标.
贝贝解二元一次方程组  得到的解是
得到的解是 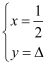 ,其中y的值被墨水盖住了,不过她通过验算求出了y的值,进而解得p的值为( )
,其中y的值被墨水盖住了,不过她通过验算求出了y的值,进而解得p的值为( )
 得到的解是
得到的解是 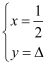 ,其中y的值被墨水盖住了,不过她通过验算求出了y的值,进而解得p的值为( )
,其中y的值被墨水盖住了,不过她通过验算求出了y的值,进而解得p的值为( )
A .  B . 1
C . 2
D . 3
B . 1
C . 2
D . 3
 B . 1
C . 2
D . 3
B . 1
C . 2
D . 3
-
(1) 解方程组:

-
(2) 已知2a-1的平方根为
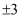 ,2a+b-1的立方根为
,2a+b-1的立方根为  ,求
,求 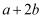 的平方根。
的平方根。
在平面直角坐标系中,点A的坐标为(m,n),若点A′(m,n′)的纵坐标满足n′= 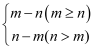 ,则称点A′是点A的“绝对点”.
,则称点A′是点A的“绝对点”.
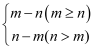 ,则称点A′是点A的“绝对点”.
,则称点A′是点A的“绝对点”.-
(1) 点(3,2)的“绝对点”的坐标为.
-
(2) 点P是函数y=4x-1的图象上的一点,点P′是点P的“绝对点”.若点P与点P′重合,求点P的坐标.
-
(3) 点Q(a,b)的“绝对点”Q′是函数y=2x2的图象上的一点.当0≤a≤2 时,求线段QQ′的最大值.
已知  ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A . 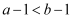 B .
B . 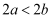 C .
C . 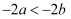 D .
D . 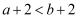
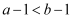 B .
B . 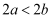 C .
C . 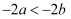 D .
D . 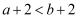
最近更新
- 关于下列图示的说法中正确的是A.用图①所示卖验可比较氯、碳、硅三种元素的非金属性强弱 B.用图②所示实验装置排空气法收集
- What shall we use for power when all the oil in the world ha
- 论语(节选)(10分)①子曰:“学而时习之,不亦说乎?有朋自远方来,不亦乐乎?人不知而不愠,不亦君子乎?”(《学而》)②
- 阅读下面文字,完成1-2题。从文化角度考察,宋词的荣耀得力于其市井文化与士林文化相互影响的双重品格。这一点,我们可以从词
- 2010年4月15日,国家科技教育领导小组会议审议并原则通过《国家中长期教育改革和发展规划纲要(2010~2020年)》
- 某生物兴趣小组利用玉米胚芽鞘做了如下图所示实验。对实验的叙述正确的是( )A.在该实验中可以不设计B琼脂块的相关实验
- (本题满分8分)随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点.据
- 已知某温度时CH3COOH的电离平衡常数为K。该温度下向20mL 0.1mol・L-1CH3COOH溶液中逐滴加入0.1
- 图反映的进步潮流出现在A.洋务运动时期 B.维新变法时期 C.辛亥革命时期 D.新文化运动时期
- (共10分)有理数、在数轴上对应点如图所示:【小题1】(1)在数轴上表示、|y|;【小题2】(2)试把、、0、、︱y︱这
- 阅读下面的科普材料。 地球上的金属资源广泛存在于地壳和海洋中,除少数很不活泼的金属如金、银等有单质形式存在外,其余都以化
- Dad is used to smoking and drinking. There’s no chance _____
- 由亍污染增多,污染物进入北极熊体内使其体型缩小;全球气候变暖,北极熊要花费更多的能量猎食.这就限制了它的生长。下列选项中
- —Thanks ______ joining the Talk Show!—You're welcome. A. b
- --- How soon will you start your journey? --- I'm not sure
- 下列语句中加点的成语使用不正确的一项是( ) A.做任何工作都不能孤军奋战,必须团结合作。众人拾柴火焰高,我们
- 27.下列关于细胞中无机物的说法正确的是( ) A.各种生物体的一切生命活动都离不开水 B.细胞中无机盐都是
- 如图,△ABC中,AD是高,CE是角平分线, AD交CE于点P,已知,∠APE=550,∠AEP=1000,求△ABC的
- 在我们身边,下列各类物质存在最多的是 A.纯净物 B.混合物 C.单质
- 燃烧产物对环境影响最小的物质是( ) A.液化气 B.煤气 C.氢气 D.天然气



