七年级(初一)数学下学期下册试题
如图所示,将 置于平面直角坐标系中,
置于平面直角坐标系中,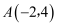 ,
, 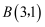 ,
, 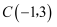 .
.
 置于平面直角坐标系中,
置于平面直角坐标系中,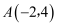 ,
, 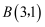 ,
, 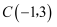 .
. 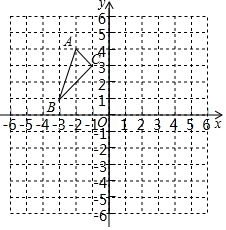
( 1 )将 先向下平移2个单位长度,再向右平移4个单位长度,画出第二次平移后的
先向下平移2个单位长度,再向右平移4个单位长度,画出第二次平移后的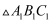 , 并写出点
, 并写出点 的坐标;
的坐标;
( 2 )以点O为对称中心,画出与 成中心对称的
成中心对称的 , 并写出点
, 并写出点 的坐标.
的坐标.
数轴上与1,  对应的点分别为A,B,点B,点A的距离与点A,点C(点C在点B的左侧)之间的距离相等,设点C表示的数为x,求代数式|x﹣2|的值.
对应的点分别为A,B,点B,点A的距离与点A,点C(点C在点B的左侧)之间的距离相等,设点C表示的数为x,求代数式|x﹣2|的值.
 对应的点分别为A,B,点B,点A的距离与点A,点C(点C在点B的左侧)之间的距离相等,设点C表示的数为x,求代数式|x﹣2|的值.
对应的点分别为A,B,点B,点A的距离与点A,点C(点C在点B的左侧)之间的距离相等,设点C表示的数为x,求代数式|x﹣2|的值. ![]()
学校为了了解七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查。根据收集的数据绘制了下面的频数分市直方图,则以下说法正确的是( )
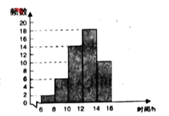
A . 绘制该频数分布直方图时选取的组距为10分成的组数为5
B . 这50人中大多数学生参加社会实践活动的时间是12-14h
C . 这50人中有64%的学生参加社会实践活动时间不少于10h
D . 可以估计全年级700人中参加社会实践活动时间为6~8h的学生大约为28人
对某班组织的一次考试成绩进行统计,已知80.5~90.5分这一组的频数是8,频率是0.2,那么该班级的人数是 人。
在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)如图,在三角形ABC中,已知∠ADE=∠B.∠1=∠2,FG⊥AB于点G,求证:CD⊥AB.
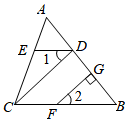
证明:∵∠ADE=∠B(已知),
∴DE∥ ▲ ( ),
∴∠1= ▲ ( ),
又∵∠1=∠2(已知),
∴ ▲ = ▲ (等量代换),
∴CD∥ ▲ ( ).
∵FG⊥AB(已知),
∴∠FGB=90°(垂直的定义),
即∠CDB=∠FGB=90°,
∴CD⊥AB(垂直的定义).
已知 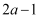 的平方根是
的平方根是 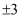 ,
,  的立方根是2,
的立方根是2,  是
是 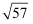 的整数部分,求
的整数部分,求 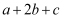 的值..
的值..
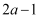 的平方根是
的平方根是 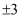 ,
,  的立方根是2,
的立方根是2,  是
是 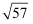 的整数部分,求
的整数部分,求 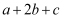 的值..
的值..
如图,已知∠ABE=72°,且∠DBF:∠ABF:∠CFB=1:2:3.
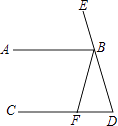
-
(1) 求∠BDC的度数;
-
(2) 若△BDF的面积为20,DF=5,求点B到直线CD的距离.
如图,  ,
, 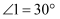 ,
, 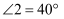 ,试求
,试求 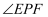 的大小.
的大小.
 ,
, 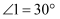 ,
, 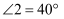 ,试求
,试求 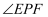 的大小.
的大小. 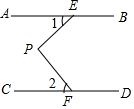
不等式组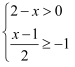 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
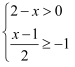 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A . 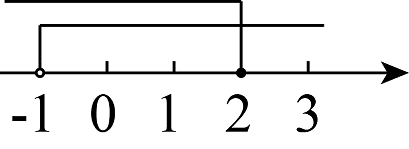 B .
B . 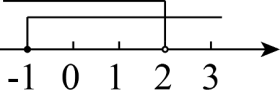 C .
C . 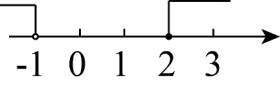 D .
D . 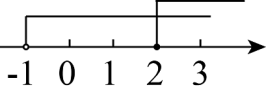
世界上最小的生物大小为 0.00000002 米,和病毒差不多大, 请用科学记数法表示 米.
已知点  是直角坐标平面内的点,如果
是直角坐标平面内的点,如果 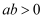 ,那么点
,那么点  在第象限.
在第象限.
 是直角坐标平面内的点,如果
是直角坐标平面内的点,如果 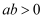 ,那么点
,那么点  在第象限.
在第象限.
每到四月,许多地方的杨絮、柳絮如雪花漫天飞舞,人们不堪其忧,据测定,杨絮纤维的直径约为0.0000115m,该数值用科学记数法表示为( )
A . 1.15×105
B . 0.115×10-4
C . 1.15×10-5
D . 115×10-7
计算:
-
(1)
 =;
=;
-
(2)
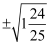 =;
=;
-
(3)
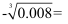 ;
;
-
(4)
 ;
;
-
(5)
 ;
;
-
(6) a3·a3=;
-
(7) (x3)5=;
-
(8) (-2x2y3)3=;
-
(9) (x-y)6÷(x-y)3=;
-
(10) a2b(ab-4b2)=
-
(11) (2a-3b)(2a+5b)=
如果关于x的不等式x≥ 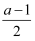 的解集在数轴上表示如图所示,那么a的值为.
的解集在数轴上表示如图所示,那么a的值为.
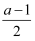 的解集在数轴上表示如图所示,那么a的值为.
的解集在数轴上表示如图所示,那么a的值为. ![]()
用计算器计算,若按键顺序为  ,相应算式是( )
,相应算式是( )
A .  ×5﹣0×5÷2=
B . (
×5﹣0×5÷2=
B . (  ×5﹣0×5)÷2=
C .
×5﹣0×5)÷2=
C . 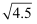 ﹣0.5÷2=
D . (
﹣0.5÷2=
D . ( 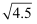 -0.5)÷2=
-0.5)÷2=
 ×5﹣0×5÷2=
B . (
×5﹣0×5÷2=
B . (  ×5﹣0×5)÷2=
C .
×5﹣0×5)÷2=
C . 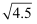 ﹣0.5÷2=
D . (
﹣0.5÷2=
D . ( 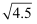 -0.5)÷2=
-0.5)÷2=
已知二元一次方程x﹣2y+1=0,用含y的代数式表示x,则x=.
下列事件是必然事件的为( )
A . 购买一张体育彩票, 中奖
B . 经过有交通信号灯的路口, 週到红灯
C . 2022 年元旦是晴天
D . 在地面上向空中抛掷一石块, 石块终将落下
已知:1纳米=1×10﹣9米.用科学记数法表示:250纳米=米.
在 中,
中,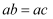 ,
, 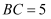 ,
, 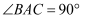 , 点D为直线BC上一动点,以AD为直角边在AD的右侧作等腰
, 点D为直线BC上一动点,以AD为直角边在AD的右侧作等腰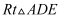 , 使
, 使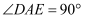 ,
, 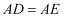 , A、E两点间的最小距离为.
, A、E两点间的最小距离为.
 中,
中,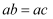 ,
, 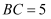 ,
, 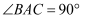 , 点D为直线BC上一动点,以AD为直角边在AD的右侧作等腰
, 点D为直线BC上一动点,以AD为直角边在AD的右侧作等腰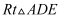 , 使
, 使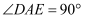 ,
, 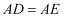 , A、E两点间的最小距离为.
, A、E两点间的最小距离为.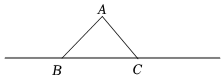
解方程组: 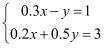
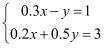
最近更新
- 对于达到平衡的反应:2A(g)+B(g) nC(g), 符合右图所示的结论是( ) A.P1>P2,n>3
- 亚硝酸可使胞嘧啶(C)变成尿嘧啶(U)。某DNA分子中的碱基对G/C中的C在亚硝酸的作用下转变成U,转变后的碱基对经过
- 阅读下面的材料,按要求作文。 有个谜语:你对它笑,它就对你笑,你对它哭,它就对你哭——这是什么? 人们都猜:这是
- ________those who lived in the slums(贫民窟), children here are
- 近年来中欧双边经贸从原有传统的、单向的贸易形式走向贸易+投资等双向的复合形态,合作领城不断从货物贸易为主转向金融服务、高
- 受各种因素影响,商品的价格千变万化。假定甲商品的原价格为每件500元,在下列各种条件下,对商品价格变动的计算正确的是 ①
- (2011年5月南通市三模4题)清人钱泳在《履园丛话》中认为:“凡置产业,自当以田地为上,市廛次之,典与铺又次之”。与此
- 结合以下图表分析,有关说法正确的是() 抗菌药物 抗菌机理 青霉素 抑制细菌细胞壁的合成
- 第II卷 (共55分) 第三部分 写作(共三节,满分55分) 第一节 单词拼写(共10小题;每小题1分,满分10分) 根
- “大力推进生态文明建设,努力建设美丽中国”是今年全国两会 的主题之一。以下行为不利于环境保护的是 A.以步代车
- 下列关于细胞学说建立过程的叙述,正确的是()A .荷兰的列文虎克发现并命名了细胞B .细胞学说揭示了生物界的统一性和差异
- 进入新世纪以来,伴随着世界多极化进程,各国目标的调整,形成了国家间既合作又竞争的局面。世界多极化不可逆转是当今国际形势的
- 根据安培定则判断得知,两根通电导线产生的磁场方向均沿逆时针方向,由于对称,两根通电导线在MN两点产生的磁感应强度大小相等
- 人们恐惧地相互看着,不知该怎么办。 People looked at each other _____________
- 综合考虑下表中几种金属的物理特性及市场价格,选用 做学生实验用组导线比较适宜(选填金属名称):高压输电线一般用
- 已知函数f(x)=|log3x|,若0<m<n且f(m)=f(n),则2m+n的取值范围为 。
- 对下列几种化学符号,有关说法正确的是 +2 ①H ②Li+ ③KClO3 ④Cu ⑤O2- ⑥Mg
- 已知1 g氢气完全燃烧生成水蒸气时放出热量121 kJ,且氧气中1 mol OO键完全断裂时吸收热量496 kJ,水蒸气
- 氯气跟碘在加热条件下,以等物质的量进行反应,可得到一种红棕色液体ICl。ICl有很强的氧化性,ICl跟Zn、H2O反应的
- 若与是同类二次根式,则a、b的值为( ) A、a=2、b=2 B、a=2、b=0 C、a=1、b=1 D、



