七年级(初一)数学下学期下册试题
计算: 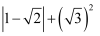 =.
=.
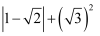 =.
=.
如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
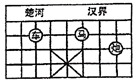
A . (2,2)
B . (-2,2)
C . (3,2)
D . (3,1)
如图,在单位正方形网格中,建立了平面直角坐标系 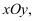 试解答下列问题:
试解答下列问题:
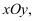 试解答下列问题:
试解答下列问题: 
-
(1) 写出
 三个顶点的坐标;
三个顶点的坐标;
-
(2) 画出
 向右平移6个单位,再向下平移2个单位后的图形
向右平移6个单位,再向下平移2个单位后的图形  ;
;
-
(3) 求
 的面积.
的面积.
一个体积为64的立方体,棱长为a,另一个面积为121的正方形,边长为b,求 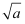 -b的相反数.
-b的相反数.
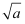 -b的相反数.
-b的相反数. 
解方程组: 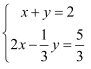 .
.
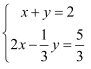 .
.
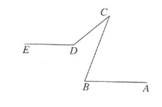
如图,已知AB∥DE,∠ABC=70°,∠CDE=140°,求∠C的度数.
计算:
-
(1) (
 )0+(
)0+(  )﹣2;
)﹣2;
-
(2) (x+y)2﹣(x﹣y)(x+y).
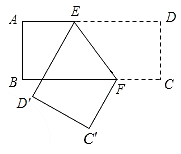
如图,把一张长方形纸条  沿
沿  折叠,若
折叠,若 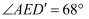 ,则
,则 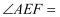 .
.
 沿
沿  折叠,若
折叠,若 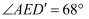 ,则
,则 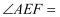 .
. 
下列说法中正确的是 ( )
A . 9的平方根是3
B . 平方根等于它本身的数是0和1
C . -2是 4的平方根
D . 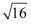 的算术平方根是4
的算术平方根是4
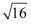 的算术平方根是4
的算术平方根是4
新冠病毒直径约为0.00000012米,这个数用科学记数法表示为.
规定一种关于a、b的新运算:a*b=b2+ab﹣a+2,那么3*(﹣2)=.
在实数  ,
, 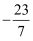 ,
,  ,0中,无理数有( )
,0中,无理数有( )
 ,
, 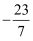 ,
,  ,0中,无理数有( )
,0中,无理数有( )
A . 1个
B . 2个
C . 3个
D . 4个
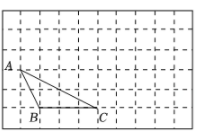
如图,在正方形网格中有一个△ABC(点A,B,C都在网格格点上),按要求完成下列各题.

-
(1) 将△ABC向右平移5格,向上平移2格,请在网格图中画出经平移后得到的△A′B′C′(点A与A′对应).
-
(2) 在(1)的基础上,连结AA′,BA′,则图中△ABA′的面积为.
下列实数中,最小的数是( )
A . 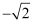 B . 0
C . 1
D . ﹣3
B . 0
C . 1
D . ﹣3
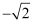 B . 0
C . 1
D . ﹣3
B . 0
C . 1
D . ﹣3
快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
-
(1) 求甲、乙两种型号的机器人每台的价格各是多少万元;
-
(2) 已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
下列各式中计算正确的是:( )
A .  B .
B . 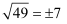 C .
C .  D .
D . 
 B .
B . 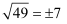 C .
C .  D .
D . 
不等式组 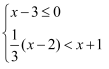 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
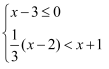 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A . 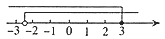 B .
B . 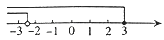 C .
C .  D .
D . 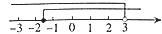
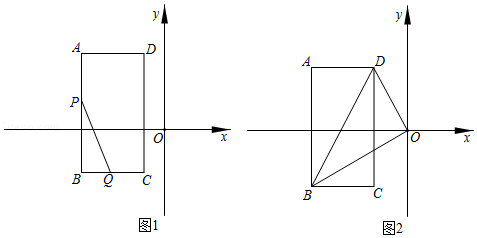
长方形ABCD位于平面直角坐标系中平行移动.
-
(1) 如图1,若AB⊥x轴且点A的坐标(﹣4,4),点C的坐标为(﹣1,﹣2),在边AB上有动点P,过点P作直线PQ交BC边于点Q,并使得BP=2BQ.
①当S△BPQ=
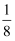 S长方形ABCD时,求P点的坐标.
S长方形ABCD时,求P点的坐标.②在直线CD上是否存在一点M,使得△MPQ是以PQ为直角边的等腰直角三角形?若存在,求出M点坐标:若不存在,请说明理由.
-
(2) 如图2,若AB⊥x轴且A、B关于x轴对称,连接BD、OB、OD,且OB平分∠CBD,求证:BO⊥DO.
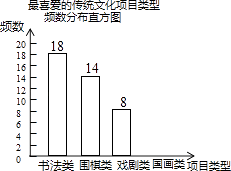
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题:
-
(1) 直接写出频数分布表中a的值;
-
(2) 补全频数分布直方图;
-
(3) 若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
点P(﹣2,1)在平面直角坐标系中所在的象限是( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
最近更新
- 如图,平行六面体ABCD—A1B1C1D1的底面ABCD是菱
- 人体泌尿系统的主要器官是( ) A.输尿
- 下列词语中加线的字注音全都正确的一组是(
- 如图装置中(烧杯中均盛有海水),铁不易被
- 下列物质分别溶于水中,温度显著升高的是(
- 生活中常接触到“加氟牙膏”、“碘盐”等用
- 将含有杂质的4.0 g的NaOH固体配成1000 mL溶液,
- 下列说法正确的是( ) A.酸只有一种分
- 下列地区,是我国热带经济作物主要产地的是
- 已知命题命题.如果同时为假命题,则满足条
- 保护环境,提高环保意识是每个公民的义务和
- 按要求完成第1—3题。 近些年来,各地兴起了
- 若直线和圆相切与点,则的值为( ) A
- 伏尔泰认为,文艺复兴的重要意义不在于“复
- 16.下面是《雷雨》中的一段台词: 周朴园
- 如图2-8-12所示的欧姆表刻度盘中,未使用时指
- 按要求作文。请以“其实,真的想 �
- (1)写出图中各仪表的读数:温度计的示数
- 美国前参议员哈特曾经说过:美国将成为“这
- 关于速度和加速度的关系,下列说法中正确的



