初中 数学
已知 , 则
, 则 的值为.
的值为.
 , 则
, 则 的值为.
的值为.
已知一个布袋里装有2个红球,3个白球和m个黄球,这些球除颜色外其余都相同,若从该布袋里任意摸出1个球,是红球的概率为 , 则m的值为 .
, 则m的值为 .
 , 则m的值为 .
, 则m的值为 .
小林所在的班级开展了分组学习竞赛活动,每次竞赛后获得前两名的小组都要颁发优胜奖状.一段时间后,老师让小林用所学的数据收集与整理知识把各组获得奖状的次数整理如下.有一些项目还没有统计完,请用现有数据帮助小林完成下面任务.
|
组 |
第一小组 |
第二小组 |
第三小组 |
第四小组 |
第五小组 |
|
次数 |
4 |
|
3 |
|
2 |

-
(1) 请将表格补充完整;
-
(2) 请将条形统计图补充完整;
-
(3) 扇形统计图中,求表示第四小组扇形的圆心角度数.
在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.

-
(1) 如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
-
(2) AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
②用等式表示线段AE与CN之间的数量关系,并证明.
如图,CD是Rt△ABC斜边AB上的高,AD=3,CD=4,则BD的长为.

平面内两个正六边形有一边AB重合在一起,将左侧的正六边形绕平面内的某一点,旋转一定的角度后能与右侧的正六边形完全重合,平面内这样的旋转中心有( )个.

A . 1
B . 3
C . 5
D . 无数
观察、思考与验证

-
(1) 如图1是一个重要公式的几何解释,请你写出这个公式 .
-
(2) 如图2所示,∠B=∠D=90°,且B,C,D在同一直线上.试说明:∠ACE=90°.
-
(3) 伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的<新英格兰教育日志》上),请你写出验证过程.
某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
-
(1) 求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
-
(2) 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
-
(3) 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
计算:
-
(1)

-
(2)

如果x是一个有理数,我们定义{x}表示不小于x的最小整数.如{3.2}=4,{﹣2.6}=﹣2,{﹣6}=﹣6.若m满足{2m+8}=6,则m的取值范围是( )
A . m≤﹣1
B . ﹣ <m≤﹣1
C . m≥﹣4
D . ﹣4≤m<﹣
<m≤﹣1
C . m≥﹣4
D . ﹣4≤m<﹣
 <m≤﹣1
C . m≥﹣4
D . ﹣4≤m<﹣
<m≤﹣1
C . m≥﹣4
D . ﹣4≤m<﹣
如图,将一个长方形  纸片沿着
纸片沿着  折叠,使
折叠,使  两点分别落在点
两点分别落在点  处.若
处.若  ,则
,则  的度数为( )
的度数为( )
 纸片沿着
纸片沿着  折叠,使
折叠,使  两点分别落在点
两点分别落在点  处.若
处.若  ,则
,则  的度数为( )
的度数为( ) 
A . 70°
B . 40°
C . 30°
D . 20°
如图,DE∥AB,FD∥BC,  ,AB=9cm,BC=6cm,则四边形BEDF的周长是多少?
,AB=9cm,BC=6cm,则四边形BEDF的周长是多少?
 ,AB=9cm,BC=6cm,则四边形BEDF的周长是多少?
,AB=9cm,BC=6cm,则四边形BEDF的周长是多少?
如图,在长方形ABCO中,点O为坐标原点,点B的坐标为(8,6),点A,C在坐标轴上,直线y=2x+b经过点A且交x轴于点F.

-
(1) 求b的值和△AFO的面积;
-
(2) 将直线y=2x+b向右平移6单位后交AB于点D,交y轴于点E;
①求点D,E的坐标;
②动点P在BC边上,点Q是坐标平面内第一象限内的点,且在平移后的直线上,若△APQ是等腰直角三角形,求点Q的坐标.
如图,在  中,
中,  ,
,  ,D是AB的中点,点E在AC上,点F在BC上,且
,D是AB的中点,点E在AC上,点F在BC上,且 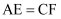 ,给出以下四个结论:(1)
,给出以下四个结论:(1)  ;(2)
;(2)  是等腰直角三角形;(3)四边形CEDF面积
是等腰直角三角形;(3)四边形CEDF面积  ;(4)
;(4)  的最小值为2.其中正确的有( ).
的最小值为2.其中正确的有( ).
 中,
中,  ,
,  ,D是AB的中点,点E在AC上,点F在BC上,且
,D是AB的中点,点E在AC上,点F在BC上,且 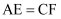 ,给出以下四个结论:(1)
,给出以下四个结论:(1)  ;(2)
;(2)  是等腰直角三角形;(3)四边形CEDF面积
是等腰直角三角形;(3)四边形CEDF面积  ;(4)
;(4)  的最小值为2.其中正确的有( ).
的最小值为2.其中正确的有( ).

A . 4个
B . 3个
C . 2个
D . 1个
2016的相反数是( )
A . 2016
B . ﹣2016
C .  D . ﹣
D . ﹣ 
 D . ﹣
D . ﹣ 
已知圆锥的侧面积为16![]() ㎝2.
㎝2.
(1)求圆锥的母线长L(㎝)关于底面半径r(㎝)之间的函数关系式;
(2)写出自变量r的取值范围;
(3)当圆锥的侧面展开图是圆心角为900的扇形时,求圆锥的高。(原创)
函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )
A.
 B.
B.
 C.
C.
 D.
D.

某商场进了一批微波炉,按进价的150%标价,春节期间,为了能吸引消费者,打8折销售,此时每台微波炉仍可获利120元,请问每台微波炉的进价是多少元?
已知反比例函数![]() ,下列结论中,不正确的是( )
,下列结论中,不正确的是( )
A. 图象必经过点(1,2) B. y随x的增大而增大
C. 图象在第一、三象限内 D. 若x>1,则0<y<2
在如图1的几何体中,它的左视图是( )
 |
最近更新
- 阅读下文,回答20~23题。 盲鳗 ①鲨鱼是海中的霸王。作为最凶猛的鱼类,鲨鱼在海底世界所向披靡,游弋所及,其它鱼
- 下图是乌鲁木齐(43°47′N)、拉萨(29°40′N)、重庆(29°31′N)和海口(20°02′N)四城市的气温、日
- 读我国某大河流域示意图,依图示信息并结合所学知识完成41~42题。 41.图中所示的河流是 A.黄河 B.淮河
- “千里之行,始于足下”、“滴水穿石”、“聚沙成塔”等成语体现的哲理是 A.要重视质的飞跃
- Don't try to get off the bus ____ it has stopped. A. while
- “今大皇帝准将香港一岛给予大英君主暨嗣后世袭主位者常远据守主掌,任便立法治理。”你认为上述内容应该出自哪个不平等条约:
- 把一个长方体切割成个四面体,则的最小值是 .
- (2010·陕西省宝鸡市高三教学质量检测三)19.I got a really good on my
- 下列实验现象描述不正确的是() A.白磷自燃产生大量的白烟 B.硫在空气中燃烧,产生淡蓝色火焰 C.细铁丝在氧气中剧烈燃
- --I heard that as many as 4 000 people were killed in 9 --Ye
- 2012年国家经济发展要求指出,经济工作要着力扩大内需特别是城乡居民消费需求。而刺激城乡居民消费必须要解决居民“有钱花”
- 近年来,《联合国反腐败公约》在预防腐败、非法资产追缴等方面取得重要进展,联合国还将每年的12月9日确定为国际反腐败日。这
- 19世纪60年代,中国和日本社会的相同点有( ) ①都与资本主义国家签订了不平等条约 ②都发生了要求改变社会性质
- 凝望自己留下的或深或浅的脚印,发现曾经行走的人生路上,竟留下了那么多值得镌刻的记忆,那是片片留在心底的风景,挥之不去,回
- 如图所示,某空间存在正交的匀强磁场和匀强电场,电场方向水平向右,磁场方向垂直纸面向里,一带电微粒由A点进入电磁场并刚好能
- 下列词语中,没有错别字的一组是A、国事 共商国是 启事 寻物启示B、编辑 开门揖盗 磨砺
- 阅读材料,回答下列问题。 材料一 科尔沁草原位于内蒙古东部,松辽平原西北部,目前大部分草地都已沙化。 材料二 1 9
- --- How longhave you worked here? --- _______I was 23 yea
- 鲁人刘仁嗜弈,然不精。一日,出市,见有人弈,观者五六,遂滞①焉。竟②局,胜者欲去,刘要之对局。胜者熟视之,曰:“善”。甫
- 将下面各项内容分别对应到政府经济职能中的相应范围,正确的是 ( )



