初中 数学
如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC= , 则BC的长是( )
, 则BC的长是( )
 , 则BC的长是( )
, 则BC的长是( )
A . 10
B . 8
C . 4 D . 2
D . 2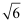
 D . 2
D . 2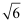
若a,b为有理数,a>0,b<0,且|a|<|b|,则a,b,-a,︱b︱的大小关系是( )
A . b<-a<︱b︱<a
B . b<-a<a<︱b︱
C . b<︱b︱<-a<a
D . -a<︱b︱<b<a
如图,甲、乙、丙、丁四个扇形的圆心角度数比为1:2:4:5,请完成下面问题:

-
(1) 求出扇形丁的圆心角度数;
-
(2) 如果圆的半径r为2,请求出扇形乙的面积.
求证:有一条直角边及斜边上的高对应相等的两个直角三角形全等.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.

-
(1) 求证:CM=CN;
-
(2) 若△CMN的面积与△CDN的面积比为3:1,求
 的值.
的值.
-6+0=
若点P(a,4-a)是第一象限的点,则a的取值范围是.
如果一组数据5、8、a、7、4的平均数是a,那么这组数据的方差为
如果2(x+3)的值与3(1﹣x)的值互为相反数,那么x等于
综合与探究.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.

-
(1) 直接写出AB的长 ;
-
(2) 点C的坐标 ,点D的坐标;
-
(3) 求直线AB的函数表达式;
-
(4) y轴上是否存在一点P,使得S△PAB=
 S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.
S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.
如图,四边形  内接于
内接于  ,
,  ,
,  ,垂足为E.
,垂足为E.
 内接于
内接于  ,
,  ,
,  ,垂足为E.
,垂足为E. 
-
(1) 若
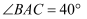 ,求
,求  的度数;
的度数;
-
(2) 求证:
 .
.
小明从正面观察如图所示的两个物体,看到的大致图形是( )

A .  B .
B .  C .
C .  D .
D . 
 C .
C .
使分式 有意义的x的取值范围为( )
有意义的x的取值范围为( )
 有意义的x的取值范围为( )
有意义的x的取值范围为( )
A . x≠2
B . x≠﹣2
C . x>﹣2
D . x<2
如图,将锐角△ABC沿DH、GF、FE翻折,三个顶点均落在点O处.若∠1=85°,则∠∠2的度数为( )

A . 75°
B . 85°
C . 90°
D . 95°
已知两个整式  ,
,  .
.
 ,
,  .
.
-
(1) 若
 的值是1,求
的值是1,求  和
和  的值;
的值;
-
(2) 若
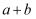 的值是0,求
的值是0,求  的值.
的值.
小明有5把钥匙,其中有2把钥匙是能打开教室门,则小明任取一把钥匙,恰好能打开教室门的概率是.
如图,  是⊙O的一条弦,
是⊙O的一条弦,  ⊥
⊥  于点C,交⊙O于点D,连接OA. 如果
于点C,交⊙O于点D,连接OA. 如果 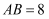 ,
,  ,那么⊙O的半径为.
,那么⊙O的半径为.
 是⊙O的一条弦,
是⊙O的一条弦,  ⊥
⊥  于点C,交⊙O于点D,连接OA. 如果
于点C,交⊙O于点D,连接OA. 如果 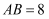 ,
,  ,那么⊙O的半径为.
,那么⊙O的半径为. 
计算(﹣3)﹣(﹣6)的结果等于( )
A . 3
B . ﹣3
C . 9
D . 18
(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;


(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上,且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.
如图,E、F是正方形ABCD的边AD上两个动点,满足AE=DF,连接CF交BD于G ,连接BE交AG于H.若正方形的边长为2
(1)求证:∠DAG=∠ABE
(2)若P是AB的中点,E在运动过程中,PH的值是否发生变化?若不变,请求出PH的![]() 值并说明理由.
值并说明理由.



图一 图二 备用图
最近更新
- As a rule, domestic servants doing odd jobs are paid ______.
- 下列四幅降水柱状图,分别表示亚洲四座城市的年降水变化,图序与城市排列顺序相符的一组是( )A.德黑兰、伊斯坦布尔、北京、
- 实验室临时需要用NaOH溶液和CO2来制取Na2CO3溶液。已知CO2气体在通入NaOH溶液时极易因其过量而生成NaHC
- 2006年5月国民党副主席江丙坤回乡祭祖,见上图。中华民族这种认祖归宗、祭拜祖宗的文化习俗最早可追溯到()A.商周时期B
- 29.阅读下列材料,回答问题。(8分) 材料一 循环经济与传统经济的比较材料二 我国人均可开采能源与世界人均值比较表石油
- --Amy put her books away just now ______ she?--Yes. I saw he
- △ABC中,AB=3,AC=4,∠A=90°,把△ABC绕直线AC旋转一周,得到一个圆锥,其表面积为S1,把△ABC绕直
- 下列物品所使用的材料中,属于有机合成材料的是() A. 钛合金表链 B. 紫砂壶 C. 手机塑料外壳 D. 真丝围巾
- 随着社会主义市场经济体制的逐步确立和国有企业改革的全面推进,社会主义民主建设已经迈开了步伐,村务公开、政务公开在不断推进
- 南京一儿科医生在工作期间玩游戏,疏于照顾病人,导致了婴儿的死亡,这引起了社会的强烈反响。这从哲学上警示我们 A.价值判断
- 泰山是我国著名的风景名山,号称五岳之首。其旭日东升、晚霞夕照、黄河金带、云海玉盘被誉为四大奇观。下图为泰山旅游线路示意图
- 准分子激光器利用氩气和氟气的混合物产生激光,用于进行近视眼的治疗,用这样的激光刀对近视眼进行手术,手术时间短,效果好,无
- Ican Diana's thoughls from thechanges in her facial
- 一个原子核内有__________个质子,__________个中子,在1 g铀235中总共有__________个质子
- 下列物质中都含有氮元素的是 ①核糖核酸 ②糖原 ③胰岛素 ④淀粉 ⑤叶绿素 A.①②
- 霜冻往往出现于深秋至第二年早春晴朗的夜晚,因为此时 A. 大气的逆辐射作用弱 B. 大气对地面辐射的吸收作用强 C.
- 宋代理学大师朱熹在任福建漳州知州时,曾为创办的白云岩书院写过一副对联:“地位清高,日月每从肩上过;门庭开豁,江山常在掌中
- 分解因式:=___________.
- 下列关于中国与APEC的关系说法正确的是 ( ) ①中国是APEC的重要成员
- 在人的体液中,CO2分压最高的是:A.组织液 B.细胞内液 C.血液 D.淋巴



