初中数学：七年级　 八年级　 九年级　 中考　

初中数学

若一次函数y＝kx＋b（k、b为常数，且k≠0）的图象经过点A（0，﹣1），B（1，1），则不等式kx＋b＜1的解为（）

A . x＜0 B . x＞0 C . x＜1 D . x＞1

$\text{[math]}$ = 。

如图，在△ABC中，AB=12，BC=10，AC=8，AD平分∠BAC交BC于点D，在AB上截取AE= AC，则 △ BDE的周长为.

如图，随机闭合开关S₁ ， S₂ ， S₃中的两个，则灯泡发光的概率是（）

图片_x0020_1490847664

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

等腰三角形的一边长是4cm，另一边长为8cm，其周长为 cm．

如图，在△ABC中，∠C=90°，D、F是AB边上的两点，以DF为直径的⊙O与BC相交于点E，连接EF，过F作FG⊥BC于点G，其中∠OFE= $\text{[math]}$ ∠A．

（1）求证：BC是⊙O的切线；
（2）若sinB= 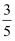$\text{[math]}$ ，⊙O的半径为r，求△EHG的面积（用含r的代数式表示）．

若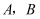 $\text{[math]}$ 互为相反数， $\text{[math]}$ 互为倒数， $\text{[math]}$ 的绝对值是2，则 $\text{[math]}$ 的值是（）

A . 2 B . 3 C . 4 D . 5

综合题。

（1） $\text{[math]}$
（2） $\text{[math]}$ ．

阅读材料：

课本中研究图形的性质，就是探究图形的构成元素（边、角、有关线段）具有怎样的特征．例如在学习等腰三角形的性质时，我们就探究得出了等腰三角形有如下性质：

边的性质：等腰三角形两腰相等；

角的性质：等腰三角形的两个底角相等；

有关线段的性质：等腰三角形顶角的平分线、底边上的高、底边的中线是同一条线段．

如果两组邻边分别相等的四边形叫筝形．如图，在四边形 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则四边形 $\text{[math]}$ 是筝形．

请探究筝形的性质，写出两条并进行证明（边的性质除外）．

图片_x0020_100034

如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高CD为米．

一个三角形的两边长分别为3cm和7cm，则此三角形的第三边的长可能是（）

A . 3cm B . 4cm C . 7cm D . 11cm

4的平方根是（）

A . ±2 B . ﹣2 C . 2 D . $\text{[math]}$

甲、乙俩射击运动员进行10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9，乙的成绩如图所示.则甲、乙射击成绩的方差之间关系是

（填“＜”，“=”，“＞”）.

图片_x0020_788678672

在Rt△ABC中,∠C=90°,若BC=10,AD平分∠BAC交BC于点D,且BD∶CD=3∶2,则点D到线段AB的距离为.

从1，2，3，4这四个数字中，任意抽取两个不同数字组成一个两位数，则这个两位数能被3整除的概率是.

如图，已知A、B、C、D是平面内四个点，请根据下列要求在所给图中作图．

①画直线AB；

②画线段BC；

③画射线AC．

今年我市参加中考的人数约是，数据用科学记数法表示为（）

A． B． C． D．

已知方程的两根为和，则=

4的算术平方根是( )

A． B． C．±2 D．2

计算（﹣3）+（﹣9）的结果是（　　）

　 A．﹣1 B．﹣6 C．+6 D． 12

最近更新

　