初中 数学
(2)n边形从一个顶点可以引出几条对角线?共有几条对角线?
 的展开式中不含
的展开式中不含  的一次项,
的一次项,  的值是.
的值是.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1 , 依此类推,排在第n位的数称为第n项,记为an .
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.
-
(1) 等比数列3,6,12,…的公比q为 ,第4项是
-
(2) 如果一个数列a1 , a2 , a3 , a4 , …是等比数列,且公比为q,那么根据定义可得到:
 =q,
=q, =q,
=q, =q,…
=q,… =q.
=q.所以:a2=a1•q,a3=a2•q=(a1•q)•q=a1•q2 , a4=a3•q=(a1•q2)•q=a1•q3 , …
由此可得:an=(用a1和q的代数式表示).
-
(3) 若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
 年
年  月份某一周每天的最高气温,如表:
月份某一周每天的最高气温,如表: | 日期 | | | | | | | |
| 最高气温 | | | | | | | |
那么这周每天的最高气温  的众数和中位数分别是( )
的众数和中位数分别是( )
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
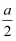 >
>  C . ﹣a<﹣b
D . 6a>6b
C . ﹣a<﹣b
D . 6a>6b

-
(1) 982(简便计算)
-
(2) (a﹣5)2﹣(a﹣2)(a+3)
-
(3) (m﹣n)2+(m﹣n)(n﹣m)
-
(4) (3m﹣2n+2)(3m+2n+2)
 ,则满足
,则满足  为整数的所有整数
为整数的所有整数  的和是( ).
的和是( ).
尺码(单位:码) | 38 | 39 | 40 | 41 | 42 |
数量(单位:双) | 2 | 5 | 3 | 1 | 2 |
则这13双运动鞋尺码的众数和中位数分别是( )
 ,则
,则  的度数为.
的度数为.
圆内接四边形ABCD中,∠A:∠B:∠C:∠D=3:5:6:m,则m= ,∠D= .
某农场去年种植了l0亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积;并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率。
若一个数的平方![]() 根是
根是![]() ,则这个数的立方根是__________ 。
,则这个数的立方根是__________ 。
将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为_________度.
 |
如图,在 

上,连接
,且

( 1 )证明: ;
( 2 )若 

重合),且
是等腰三角形,求此时


- 下列实验操作正确且能达到相应实验目的的是() 实验目的 实验操作 A 称取2.0 g NaOH固体 先在托盘上各放1张滤
- 当DNA分子的一条单链中(A+T)/(G+C)=0.7时,在整个DNA分子中这种比例是 A.1.43 B.
- 如图,将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠,使点A与BC边上的点E重合,折痕交AB于点F.若
- 能量是生物体进行生命活动的动力。生物体主要的供能物质是 A.糖类 B.脂肪 C.蛋白质
- 已知及所在平面一点,符合条件:,且,则的形状为( ) A 正 B等腰 C直角 D
- 柴达木盆地以青藏高原“聚宝盆”之誉蜚声海内外,它有富足得令人惊讶的盐矿资源。液体矿床以钾矿为主,伴生着镁、溴等多种矿产。
- .某网站上为纪念“百日维新”115周年而展开了大讨论,下面观点不正确的是 A.戊戌变法运动最突出的历史作用在于促进思想启
- 根据我国古代流传的天干、地支、属相都可以表示一个人的生日.据你的出生年月,可以知道你是哪个星座.我们知道3月21日到4月
- 某小区有些居民晚上经常一起打牌娱乐,影响了一张姓居民的正常休息并引发争执,居民委员会就此召开居民会议,通过表决,会议作
- 在一定温度下,体积固定的密闭容器中,发生如下的反应:N2(g)+3H2(g) 2NH3(g) △H<0下列叙述不能证明
- .某基态原子核外共有6个电子,分布在K与L电子层上,则下列L层电子排布图中正确的是( ) A. B.
- 常温下,在溶液中发生如下反应:①16H++10Z-+2XO===2X2++5Z2+8H2O ②2A2++B2===2A3
- He is familiar _____ this place, because he used to live in
- 下列句子没有语病的一项是( )(2分) A.在节约型社会里,人们有效利用资源进一步增强。 B.这篇小说完美地塑造了
- 北宋时期与之并存的少数民族政权的疆域为“东尽黄河,西界玉门,南接萧关(甘肃固原东南),北控大漠,地方万余里”,这个少数民
- Sandy didn’t tell her parentsthat she was going home because
- 如图,在四面体中,已知、、两两互相垂直,且.则在该四面体表面上与点距离为的点形成的曲线段的总长度为 A.
- 依次填入下列各句子中横线处的词语,最恰当的一项是 ①我有时把手放在我的胸膛上,我知道我的心还是跳动的,我的心还在喷涌着热
- 唐太宗时期,假设国家要在关中一带修建一项大型水利工程,这项工程的实施涉及众多机构,按制度规定其运作程序是 A.尚书省
- 在物理学发展的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法正确的是












