初中 数学
在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤  .其中正确的个数为( ).
.其中正确的个数为( ).
 .其中正确的个数为( ).
.其中正确的个数为( ). 
A . 2
B . 3
C . 4
D . 5
已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,则a的取值范围是( )
A . a>2
B . a<2
C . a<2且a≠l
D . a<﹣2
阅读材料:在实数范围内,当  且
且  时 ,我们由非负数的性质知道
时 ,我们由非负数的性质知道  ,所以
,所以  , 即:
, 即:  ,当且仅当
,当且仅当  =
=  时,等号成立,这就是数学上有名的“均值不等式”,若
时,等号成立,这就是数学上有名的“均值不等式”,若  与
与  的积为定值
的积为定值  . 则
. 则 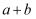 有最小值
有最小值  :请问: 若
:请问: 若  , 则当
, 则当  取何值时,代数式
取何值时,代数式  取最小值? 最小值是多少?
取最小值? 最小值是多少?
 且
且  时 ,我们由非负数的性质知道
时 ,我们由非负数的性质知道  ,所以
,所以  , 即:
, 即:  ,当且仅当
,当且仅当  =
=  时,等号成立,这就是数学上有名的“均值不等式”,若
时,等号成立,这就是数学上有名的“均值不等式”,若  与
与  的积为定值
的积为定值  . 则
. 则 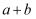 有最小值
有最小值  :请问: 若
:请问: 若  , 则当
, 则当  取何值时,代数式
取何值时,代数式  取最小值? 最小值是多少?
取最小值? 最小值是多少?
先化简,再求值:[1+  ]÷
]÷  ,其中x=6.
,其中x=6.
 ]÷
]÷  ,其中x=6.
,其中x=6.
阅读与思考:
正方形还有许多有趣的性质,下面是小宇同学找到的有关正方形的几个图形,想一想其中的道理.

如图①,在正方形  中,点
中,点  、
、  、
、  分别是边
分别是边  、
、  ,
,  上的点.
上的点.
-
(1) 获得发现:如图①,当
 时,则有
时,则有  ;如图②,当
;如图②,当  时,则有
时,则有  ;如图③,当
;如图③,当  时,则有
时,则有  .想一想,这是为什么?结合图②给出证明.
.想一想,这是为什么?结合图②给出证明.
-
(2)
解决问题:如图④,在正方形
 中,点
中,点  在边
在边  上(点
上(点  与点
与点  、
、  不重合),过点
不重合),过点  作
作  ,
,  与边
与边  相交于点
相交于点  ,与边
,与边  的延长线相交于点
的延长线相交于点  .
.
猜想线段
 、
、 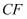 、
、  的数量关系是 , 并证明你的猜想;
的数量关系是 , 并证明你的猜想;
-
(3) 连接
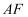 ,如果正方形的边长为2,设
,如果正方形的边长为2,设  ,
,  的面积为
的面积为  ,直接写出
,直接写出  与
与  之间的关系式,并写出自变量
之间的关系式,并写出自变量  的取值范围.
的取值范围.
如图,已知抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中B点的坐标为(3,0).

-
(1) 直接写出A点的坐标;
-
(2) 求二次函数y=ax2+bx﹣3的解析式.
细菌分裂是一种特殊的生殖方式,细菌分裂一次由一个变为两个.某种细菌每半个小时便可以进行一次分裂,经过5小时后这种细菌由1个能分裂成个.
计算 的结果是 ( )
的结果是 ( )
 的结果是 ( )
的结果是 ( )
A .  B .
B .  C .
C . 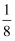 D .
D . 
 B .
B .  C .
C . 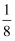 D .
D . 
如图所示,DE是△ABC的中位线,BC=8,则DE=.

如图所示,将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B1 , C1在同一条直线上,则∠AEF=.

如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,AB∥CD∥EF,AF∥CG,则图中与∠A(不包括∠A)相等的角有( )

A . 5个
B . 4个
C . 3个
D . 2个
小球从离地面为h(单位:m)的高处自由下落,落到地面所用时间为t(单位:s),经过实验,发现h与  成正比例关系,当
成正比例关系,当  时,
时,  ,则当
,则当  时,t的值是.
时,t的值是.
 成正比例关系,当
成正比例关系,当  时,
时,  ,则当
,则当  时,t的值是.
时,t的值是.
如图,CD是⊙O的直径,A、B是⊙O上的两点,若∠ABD=20°,则∠ADC的度数为( )

A . 40°
B . 50°
C . 60°
D . 70°
对于每个正整数n,设f(n)表示n(n+1)的末位数字.例如:f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),…则f(1)+f(2)+f(3)+…f(2022)的值为( )
A . 4042
B . 4048
C . 4050
D . 10
二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,AB∥CD,点E在BC上,CD=CE,若∠ABC=34°,则∠BED的度数是( )

A . 104°
B . 107°
C . 116°
D . 124°
某校女子排球队队员的年龄分布如下表
| 年龄(岁) | 13 | 1 | 15 |
| 人数(人) | 4 | 7 | 4 |
则该校女子排球队队员的平均年龄是______岁
要使分式![]()
![]() 的值为零,则x= .
的值为零,则x= .
已知⊿ABC,∠C=90°,一条直角边AC=10cm,斜边AB=26cm,则斜边上的高CD=___________cm.

最近更新
- 补写出下列名篇名句中的空缺部分。(两题任选一题) (1)君不见黄河之水天上来,______________。君不见高堂明
- 读下列俄罗斯与澳大利亚自然地理分布简图,回答相关问题:(1)俄罗斯自然地理分布图中,图例ABC所表示的自然环境要素是
- (1)写出下列烷烃:分子中有26个电子的结构简式 。 分子中含25个化学键的分子式 ,支链含乙基
- 《圣经》把两河流域描绘成“人类幸福的伊甸园”.在这里曾经孕育的文明国度是() A.古巴比伦 B.古代埃及
- 近年来,“晒黑族”异军突起,他们将社会上的不平事在网上进行披露,以警醒其他网民或政府部门,推动问题的解决。“晒黑族”的一
- 下面四图是来自于同一生物体内的、处于四个不同状态的细胞分裂图像。下列有关叙述中,正确的是()A.该生物的正常体细胞中含有
- 化学反应前后没有发生改变的是() ①元素的种类;②原子的种类;③原子的个数;④原子的质量;⑤物质的总质量;⑥分子的种类;
- 直线(t为参数)的倾斜角α等于() A.30°B.60°C.-45°D.135°
- 阅读下面一段文字: 聚苯乙烯快餐盒、一次性塑料包装袋和聚氯乙烯农用地膜被视为危害环境的三大“白色公害”。
- 世界上大多数的农作物和动植物都能在我国找到适合生长的地方,这是因为我国() A.季风气候显著 B.气候复杂多
- 中新网2008年3月11日电,著名呼吸专家,中国工程院院士钟南山称SARS已经过去5年,仍不清楚其最终源头。SARS病毒
- 3.植物组织培养的用途中不正确的是:( ) A.快速繁殖 B.生产新品种 C.生产生物碱 D.生产白细胞介素-2
- 下列图示中的水,可以看作纯净物的是 A.河湖水 B.温泉水 C.蒸馏水 D.自来水
- 卡车原来用10 m/s的速度匀速在平直公路上行驶,因为路口出现红灯,司机从较远的地方即开始刹车,使卡车匀减速前进.当车减
- 根据图示填空(1)化合物A含有的官能团 。
- 对大城市交通民警危害最大的污染物是 A.煤烟、粉尘 B.工业废水 C.碳氢化合物和氮氧化合物
- 下列说法中正确的是 (
- 万里长征是中国工农红军进行的伟大战略转移。这里的“转移”是指 A.中国革命性质发生了变化 B.党的工作重心发生了转移 C
- 化学与生活、社会密切相关。下列说法不正确的是( ) A.利用太阳能等清洁能源代替化石燃料,有利于节约资源、保护环境
- “速度、质量、效益相协调;消费、投资、出口相协调;人口、资源、环境相协调。”这三个“相协调”最能反映的是 A.可持续发展



