初中 数学
如图,点A在双曲线  上,连接
上,连接  ,作
,作  ,交双曲线
,交双曲线  于点B , 连接
于点B , 连接  .若
.若  ,则k的值为( )
,则k的值为( )
 上,连接
上,连接  ,作
,作  ,交双曲线
,交双曲线  于点B , 连接
于点B , 连接  .若
.若  ,则k的值为( )
,则k的值为( ) 
A . 1
B . 2
C .  D .
D . 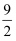
 D .
D . 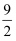
抛物线  的顶点坐标是( )
的顶点坐标是( )
 的顶点坐标是( )
的顶点坐标是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
反比例函数  (k为不等于0的常数)的图象如图所示,以下结论错误的是( )
(k为不等于0的常数)的图象如图所示,以下结论错误的是( )
 (k为不等于0的常数)的图象如图所示,以下结论错误的是( )
(k为不等于0的常数)的图象如图所示,以下结论错误的是( ) 
A . k>0
B . 若点M (1,3)在图象上,则k=3
C . 在每个象限内,y的值随x值的增大而增大
D . 若点A(-1,a),B(2,b)在图象上,则a<b
如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断  和
和  是否相等,并说明理由.
是否相等,并说明理由.
 和
和  是否相等,并说明理由.
是否相等,并说明理由.
2019年国庆假日七天里,民航提供的运力满足了旅客出行需求,中国民航共保障国内外航班1280万余次,将1280万用科学记数法表示应为( )
A . 0.128×1011
B . 1.28×107
C . 1.78×103
D . 12.8×106
如图,在△ABC中,∠ACB=90°,将△ABC绕着点A逆时针旋转得到△ADE,点C落在边AD上,连接BD.若∠DAE=α,则用含α的式子表示∠CBD的大小是( )

A . α
B . 90°﹣α
C .  D .
D . 

 D .
D . 

如图,在平面直角坐标系  中,点
中,点  在反比例函数
在反比例函数  的图象上,点
的图象上,点  在
在  的延长线上,
的延长线上,  轴,垂足为
轴,垂足为  ,
,  与反比例函数的图象相交于点
与反比例函数的图象相交于点  ,连接
,连接  ,
,  .
.
 中,点
中,点  在反比例函数
在反比例函数  的图象上,点
的图象上,点  在
在  的延长线上,
的延长线上,  轴,垂足为
轴,垂足为  ,
,  与反比例函数的图象相交于点
与反比例函数的图象相交于点  ,连接
,连接  ,
,  .
. 
-
(1) 求该反比例函数的解析式;
-
(2) 若
 ,设点
,设点  的坐标为
的坐标为  ,求线段
,求线段  的长.
的长.
观察下列各式:
 ;
;  ;
;  ;
;
…
请你根据以上三个等式提供的信息解答下列问题
-
(1) 猜想:
 ==;
==;
-
(2) 归纳:根据你的观察,猜想,请写出一个用n(n为正整数)表示的等式:;
-
(3) 应用:计算
 .
.
将抛物线  向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为.
向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为.
 向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为.
向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为.
如图,在正方形 ABCD ,E是对角线 BD 上一点, AE 的延长线交 CD 于点F , 连接 CE .若∠BAE=56° ,则 ∠CEF= ° .

妈妈炖了一锅鸡汤,先用小勺舀了一点尝尝味道,这是利用了的思想.
如果今年国庆节是星期四,那么明年的国庆节是星期六.
某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

-
(1) 本次调查样本容量为;
-
(2) 在频数分布表中,a= ▲ , b= ▲ , 并将频数分布直方图补充完整;
-
(3) 若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?
在平面直角坐标系中有两条直线:  和
和  ,它们的交点为点P,且它们与
,它们的交点为点P,且它们与  轴的交点分别为A、B.
轴的交点分别为A、B.
 和
和  ,它们的交点为点P,且它们与
,它们的交点为点P,且它们与 -
(1) 在同一坐标系中作出两条直线的图象;
-
(2) 求A、B两点的坐标和△PAB的面积.
任何一个有理数的4次幂都是( )
A . 正数
B . 负数
C . 非负数
D . 任何有理数
如图①,在半径为6的扇形AOB中, 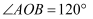 ,点C是弧AB上的一个动点(不与点
,点C是弧AB上的一个动点(不与点  、
、  重合),
重合),  、
、  ,垂足分别为D、E.
,垂足分别为D、E.
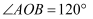 ,点C是弧AB上的一个动点(不与点
,点C是弧AB上的一个动点(不与点  、
、  重合),
重合),  、
、  ,垂足分别为D、E.
,垂足分别为D、E. 
-
(1) ①当
 时,线段
时,线段  ;
; ②当
 的度数=°时,四边形
的度数=°时,四边形  成为菱形;
成为菱形; -
(2) 试说明:四边形
 的四个顶点在同一个圆上;
的四个顶点在同一个圆上;
-
(3) 如图②,过点
 作
作  ,垂足为
,垂足为  ,连接
,连接 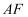 ,随着点
,随着点  的运动,在△
的运动,在△  中是否存在保持不变的角?如果存在,请指出这个角并求出它的度数;如果不存在,请说明理由;
中是否存在保持不变的角?如果存在,请指出这个角并求出它的度数;如果不存在,请说明理由;
-
(4) 在(3)条件下,若点
 从点
从点  运动到点
运动到点  ,则点
,则点  的运动路径长为.
的运动路径长为.
计算:(﹣1)2019+  +(
+(  )﹣1
)﹣1
 +(
+(  )﹣1
)﹣1
已知关于x的函数y=(m+2)x2+2x﹣1与x轴仅有一个公共点,则m等于
如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对![]() 折,使A、C重合,直线MN交AC于O.
折,使A、C重合,直线MN交AC于O.
(1)、求证:△COM∽△CBA;
(2)、求线段OM的长度.

已知一个Rt△的两边长分别为3和4,则第三边是 .
最近更新
- (5分)用50mL0.50mol/L盐酸与50mL0.55mol/LNaOH溶液在如图所示的装置中进行中和反应。通过测定
- .I don’t suppose they’ll be seeing each other very often sin
- 氢化铵(NH4H)与氯化铵的结构相似,又知NH4H与水反应有H2生成,下列叙述不正确的是
- 根据相关的化学原理,下列判断正确的是( ) A.由于水中存在氢键,所以稳定性:H2O>H2S B.由于二氧化硅的相对
- We have every reason to believe the print media are usually
- 下列各组函数是同一函数的是 ( ) ①与; ②与; ③与; ④与。 A、①
- 阅读下面划横线的句子,根据要求写一篇不少于800字的文章。 一位科学家结合自己所学专业和人生总结出这样的话:“做功
- 国务院总理温家宝在十一届全国人大二次会议上所作的《政府工作报告》中指出:2009年的政府工作,要以应对国际金融危机、
- 将一物体以水平速度v0抛向一个倾角为α的斜面,物体与斜面相撞时的速度与斜面交角为β,如图9,求抛出到与斜面相撞所经时间t
- 读图我国某气象灾害平均每年出现次数的分布图,完成下列问题。14.如图反映的自然灾害是() A. 干旱 B. 台风
- 把一片刚摘下的叶片浸在盛有70℃左右热水的烧杯中,会看到叶片的表面产生许多的气泡,而且实验显示叶片背面产生的气泡比正面多
- 直线y=x+b交抛物线于A、B两点,O为抛物线的顶点,若OA⊥OB,则b=_______.
- 2014年我国1000万套保障性住房陆续上市,一线城市商品房价格回落,新楼盘开盘减少。下图中Q1为变化前新上市商品房数量
- 在一个6L的密闭容器中放入3mol X和2molY,在一定条件下发生反应4X(g)+3Y(g) 2Q(g) +
- 正确表示光从空气进入玻璃中的光路是
- 海带中含碘元素,从海带中提取碘有如下步骤:①通入足量Cl2 ②将海带焙烧成灰后加水搅拌 ③加CCl4振荡 ④用分
- 下列对生物体的结构层次和功能的描述,其中不正确的一项是A.构成水稻的结构和功能的基本单位是细胞B.牛的结构层次为细胞→组
- 2010年5月,中央新疆工作座谈会上强调,做好新形势下的新疆工作,必须始终把握各民族共同团结奋斗、共同繁荣发展的主题。新
- Many women today hold that it’s their husbands’ responsibili
- 小明发现菜地里许多植物出现倒伏现象,并伴有叶色发黄,植株矮小现象。现有氯化铵、尿素、磷矿粉、硝酸钾、氯化钾等,请帮助他选



