初中 数学
如图,  是
是  的直径,
的直径,  是弦
是弦  的中点,
的中点,  于点
于点  ,若
,若 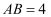 ,
,  ,则
,则  的长为( )
的长为( )
 是
是  的直径,
的直径,  是弦
是弦  的中点,
的中点,  于点
于点  ,若
,若 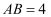 ,
,  ,则
,则  的长为( )
的长为( )

A .  B . 1.5
C .
B . 1.5
C .  D . 2
D . 2
 B . 1.5
C .
B . 1.5
C .  D . 2
D . 2
如图,在Rt△ABC中,  现在有一足够大的直角三角板,它的直角顶点D是BC边上一点,另两条直角边分别交AB、AC于点E、F.
现在有一足够大的直角三角板,它的直角顶点D是BC边上一点,另两条直角边分别交AB、AC于点E、F.
 现在有一足够大的直角三角板,它的直角顶点D是BC边上一点,另两条直角边分别交AB、AC于点E、F.
现在有一足够大的直角三角板,它的直角顶点D是BC边上一点,另两条直角边分别交AB、AC于点E、F. 
-
(1) 如图1,若DE⊥AB,DF⊥AC,求证:四边形AEDF是矩形
-
(2) 在(1)条件下,若点D在∠BAC的角平分线上,试判断此时四边形AEDF形状,并说明理由;
-
(3) 若点D在∠BAC的角平分线上,将直角三角板绕点D旋转一定的角度,使得直角三角板的两条边与两条直角边分别交于点E、F(如图2),试证明
 .(尝试作辅助线)
.(尝试作辅助线)
已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F.
求证:AB=BF.

方孔钱是我国古代铜钱的固定形式,呈“外圆内方”.如图所示,是方孔钱的示意图,已知“外圆”的周长为2π,“内方”的周长为4,则图中阴影部分的面积是.

如图,已知线段  ,利用尺规作
,利用尺规作  的垂直平分线,步骤如下:①分别以点
的垂直平分线,步骤如下:①分别以点  为圆心,以
为圆心,以  的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点  和
和  .②作直线
.②作直线  .直线
.直线  就是线段
就是线段  的垂直平分线.则
的垂直平分线.则  的长可能是( )
的长可能是( )
 ,利用尺规作
,利用尺规作  的垂直平分线,步骤如下:①分别以点
的垂直平分线,步骤如下:①分别以点  为圆心,以
为圆心,以  的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点  和
和  .②作直线
.②作直线  .直线
.直线  就是线段
就是线段  的垂直平分线.则
的垂直平分线.则  的长可能是( )
的长可能是( ) 
A . 1
B . 2
C . 3
D . 4
如图,点P在ΔABC的边AC上,下列条件中不能判定 的是( )
的是( )
 的是( )
的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
一元二次方程x2+5x+7=0解的情况是( )
A . 有两个不相等的实数根
B . 有两个相等的实数根
C . 没有实数根
D . 无法确定
若将分式 中的
中的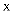 和
和 都扩大到原来的10倍,则分式的值( )
都扩大到原来的10倍,则分式的值( )
 中的
中的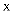 和
和 都扩大到原来的10倍,则分式的值( )
都扩大到原来的10倍,则分式的值( )
A . 缩小到原来的 B . 不变
C . 扩大到原来的10倍
D . 缩小到原来的
B . 不变
C . 扩大到原来的10倍
D . 缩小到原来的
 B . 不变
C . 扩大到原来的10倍
D . 缩小到原来的
B . 不变
C . 扩大到原来的10倍
D . 缩小到原来的
某童装专卖店,为了吸引顾客,在“六一”儿童节当天举办了甲、乙两种品牌童装有奖酬宾活动,凡购物满100元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同.摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如表).
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满100元,若只考虑获得最多的礼品券,请你帮助分析选择购买哪种品牌的童装?并说明理由.
甲种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 15 | 30 | 15 | |
乙种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 30 | 15 | 30 |
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.

-
(1) 求证:BE=CE
-
(2) 如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
-
(3) 在(2)的条件下,若∠BAC=45
 ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.
比较大小: 
 .(填“<“,“=“,“>“)
.(填“<“,“=“,“>“)

 .(填“<“,“=“,“>“)
.(填“<“,“=“,“>“)
如图,其中所有三角形都是直角三角形,所有四边形都是正方形.若S1=4,S2=9,S3=8,S4=10,则S等于( )

A . 25
B . 31
C . 32
D . 40
等边三角形的边长是4,则高AD  (结果精确到0.1)
(结果精确到0.1)
 (结果精确到0.1)
(结果精确到0.1)
如图,在四边形ABCD中,AD  BC,AB= AD,∠BAD的平分线交BC于点E,连结DE.
BC,AB= AD,∠BAD的平分线交BC于点E,连结DE.
 BC,AB= AD,∠BAD的平分线交BC于点E,连结DE.
BC,AB= AD,∠BAD的平分线交BC于点E,连结DE. 
-
(1) 求证:四边形ABED是菱形.
-
(2) 连结BD.若CE=2BE,AE=4,BD=6,则△CDE的面积是 .
若n边形恰好有n条对角线,则n=.
若![]() +
+![]() =0,则x= 。
=0,则x= 。
解不等式:![]() ≤
≤![]() ﹣1,并把解集表示在数轴上.
﹣1,并把解集表示在数轴上.
一个圆柱的底面周长是12.56厘米,高是6厘米,那么底面半径是 厘米,底面积是 平方厘米,侧面积是 平方厘米,体积是 立方厘米.将它削成一个最大的圆锥体,应削去 立方厘米.
某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
如图,将△EAB绕正方形ABCD的顶点A逆时针旋转90°,得到△DAF,连接EF,则下列结论错误的是( )
A.△EAB≌△FAD B.AE⊥AF
C.∠AEF=45° D.四边形AECF的周长等于ABCD的周长
最近更新
- He knows so much about the story. He must have read the book
- 阅读下面的语段,结合全文内容,回答16一19题。这是一只光秃秃没剩几根毛的母鸡,人们再也不可能见到比它更老、更瘦的鸡了.
- 我国有文字可考的历史是从商朝开始,主要证据是 ( )
- 如图所示中图线①表示某电池组的输出电压—电流关系,图线②表示其输出功率—电流关系.根据图线可以求出A.电源电动势. B.
- —Who is thegirl under the tree? — She be Lucy. She
- 已知函数(是常数,≠0),下列结论正确的是 A. 当时,函数图象过点(-1,1) B. 当时,函数图象与轴没有交点 C
- 读图回答下列问题:(10分)(1)海洋灾害除了赤潮现象,还有 ▲ 、 ▲ 等自然灾害。(2分) (2)201
- What shall we use for power when all the oil in the world ha
- 读右图,回答下列问题。(8分)(1)从图A中可以看出:夏威夷群岛位于洋的北部,属于 国和 洲, 以
- 1945年夏,一架横渡太平洋的客机不幸中途失事,部分乘客漂流到一个荒无人烟、寸草不生的孤岛上,并最终得以生还。在等待救
- It was__ he said__ disappointed me.A. that;what B. what;th
- After four months of investigating, she was found guilty, an
- (满分16分)记函数f(x)的定义域为D,若存在,使成立,则称以为坐标的点为函数图象上的不动点。 (1)若函数的图象上有
- 东南亚成为世界重要的热带作物生产基地之一,最主要的条件是() A.气候湿热 B.平原广大
- Mustafa Kemal Atatürk,the founder of the Turkish Republic, d
- 数十亿年来,地球上的物质不断地变化。大气的成分也发生了很大的变化。 下表是原始大气和目前空气的主要成分:空气的成分 N2
- 设NA为阿伏加德罗常数的值,下列叙述正确的是A.常温常压下,16g14CH4所含中子数目为8NAB.标准状况下,22.4
- 在“探究并联电路电流的特点”实验中,实验电路如图甲所示,闭合开关S后,电流表A1、A2示数分别如图乙、丙所示,则通过灯泡
- 一个边长为4㎝的等边三角形与⊙等高,如图放置, ⊙与相切于点,⊙与相交于点,则的长为 ㎝.
- △ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件 ,若加条件∠B=∠



