初中 数学
分解因式:2x2y﹣8y=.
如图,在 中,
中, , AD平分
, AD平分 ,
,  于点E,若
于点E,若 , 则BE的长为( )
, 则BE的长为( )
 中,
中, , AD平分
, AD平分 ,
,  于点E,若
于点E,若 , 则BE的长为( )
, 则BE的长为( )
A . 5
B . 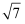 C .
C . 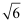 D . 2
D . 2
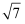 C .
C . 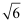 D . 2
D . 2
对某班最近一次数学测试成绩  得分取整数
得分取整数  进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为A等
进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为A等  分以上,不含80分
分以上,不含80分  的百分率为
的百分率为  精确到
精确到 
 得分取整数
得分取整数  进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为A等
进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为A等  分以上,不含80分
分以上,不含80分  的百分率为
的百分率为  精确到
精确到 

平移和旋转都不改变图形的 和 .
如图,在△ABC中,AB=BC,∠ABC=100°,边BA绕点B顺时针旋转m°,(0<m<180)得到线段BD,连接AD、DC,若△ADC为等腰三角形,则m所有可能的取值是.

点P在第四象限,且点P到x轴的距离为3,点P到y轴的距离为2,则点P的坐标为( )
A . (-3,-2)
B . (3,-2)
C . (2,3)
D . (2,-3)
-
(1) 先化简
 ,再选择一个合适的x值代入求值.
,再选择一个合适的x值代入求值.
-
(2) 如图所示,已知点A , D , B , E在同一条直线上,且AD=BE , BC=EF , ∠ABC=∠DEF , 求证:AC∥DF .

在平面直角坐标系中(单位长度为1cm),已知点A(0,m),N(n,0),且  +|m+n﹣10|=0.
+|m+n﹣10|=0.
 +|m+n﹣10|=0.
+|m+n﹣10|=0. 
-
(1) m= ,n= .
-
(2) 如图,若点E是第一象限内的一点,且EN⊥x轴,过点E作x轴的平行线a,与y轴交于点A,点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.
①经过几秒PQ∥y轴?
②若某一时刻以A、O、Q、P为顶点的四边形的面积是10cm2 , 求此时点P的坐标.
a与b的平方的和用代数式表示为 ( )
A . a+b2
B . (a+b) 2
C . a2+b2
D . a2+b
如图,在 中,
中,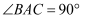 , 点
, 点 ,
,  分别是
分别是 ,
,  的中点,点
的中点,点 在
在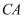 的延长线上,
的延长线上, ,
,  ,
, 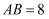 , 则四边形
, 则四边形 的周长为( )
的周长为( )
 中,
中,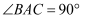 , 点
, 点 ,
,  分别是
分别是 ,
,  的中点,点
的中点,点 在
在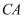 的延长线上,
的延长线上, ,
,  ,
, 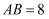 , 则四边形
, 则四边形 的周长为( )
的周长为( )
A . 14
B . 16
C . 18
D . 20
如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.

-
(1) 求点A、B、C的坐标;
-
(2) 点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
-
(3) 在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若,
 求点F的坐标.
求点F的坐标.
阅读理解题:
学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2  =(1+
=(1+  )2 , 我们来进行以下的探索:
)2 , 我们来进行以下的探索:
设a+b  =(m+n
=(m+n  )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b  =m2+2n2+2mn
=m2+2n2+2mn  ,∴a=m+2n2 , b=2mn
,∴a=m+2n2 , b=2mn
, 这样就得出了把类似a+b  的式子化为平方式的方法.
的式子化为平方式的方法.
请仿照上述方法探索并解决下列问题:
-
(1) 当a,b,m,n都为正整数时,若a﹣b
 =(m﹣n
=(m﹣n  )2 , 用含m,n的式子分别表示a,b,得a=,b=;
)2 , 用含m,n的式子分别表示a,b,得a=,b=;
-
(2) 利用上述方法,找一组正整数a,b,m,n填空:﹣
 =(﹣
=(﹣  )2
)2
-
(3) a﹣4
 =(m﹣n
=(m﹣n  )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
已知三项式9x2+1+  是一个完全平方式,但是其中一项看不清了,你认为这一项应该是(写出一个所有你认为正确的答案).
是一个完全平方式,但是其中一项看不清了,你认为这一项应该是(写出一个所有你认为正确的答案).
计算: 

如图,在四边形  中,
中,  ,过点
,过点  作
作  ,交
,交  于点
于点  ,连接
,连接  ,
,  ,若
,若  ,则
,则  .
.
 中,
中,  ,过点
,过点  作
作  ,交
,交  于点
于点  ,连接
,连接  ,
,  ,若
,若  ,则
,则  .
. 
如图,⊙O的圆心O在△ABC的边AC上,AC与⊙O分别交于C,D两点,⊙O与边AB相切,且切点恰为点B.

-
(1) 求证:∠A+2∠C=90°;
-
(2) 若∠A=30°,⊙O的半径为2,求图中阴影部分的面积.
某中学有一块四边形的空地 , 如下图所示,学校计划在空地上种植草皮,经测量
, 如下图所示,学校计划在空地上种植草皮,经测量 ,
,  ,
,  ,
,  ,
,  , 若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
, 若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
 , 如下图所示,学校计划在空地上种植草皮,经测量
, 如下图所示,学校计划在空地上种植草皮,经测量 ,
,  ,
,  ,
,  ,
,  , 若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
, 若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
计算:
-
(1) 22+(﹣4)+(﹣2)+4
-
(2) (﹣
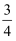 +1
+1  ﹣
﹣  )×(﹣24)
)×(﹣24)
-
(3) 3﹣6÷(﹣2)×|﹣
 |
|
-
(4) 2a﹣(3b﹣a)+b
-
(5) 3(x2﹣y2)+(y2﹣z2)﹣2(z2﹣y2)
-
(6) (﹣
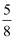 )×(﹣4)2﹣0.25×(﹣5)×(﹣4)3 .
)×(﹣4)2﹣0.25×(﹣5)×(﹣4)3 .
点 所在的象限为( )
所在的象限为( )
 所在的象限为( )
所在的象限为( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
化简![]() =________
=________
最近更新
- DNA分子的一条链中(A+G)/(T+C)=0.4,上述比例在其互补链和整个DNA分子中分别是A. 0.4和0.6
- 劳动者是创造商品价值的主体,对劳动者的尊重和保护是提升全社会人力资源价值的重要举措。根据法律规定,用人单位有义务保障职工
- 下列实验操作中正确的是 A.向试管中滴加液体时,滴管应垂悬在试管口上方,并不接触试管 B.实验用剩的药品应放回原试
- A team of researchers at the University of Illinois at C
- 我们平时饮用的葡萄酒呈红色,其原因是 A.酒精发酵前榨汁时榨出的红色葡萄皮中的色素 B.是红色葡萄球菌分泌的色素 C.在
- A warm thought suddenly cameto me _______ I might use my po
- Tom watches TV four __________ five ________a week. A. and,
- 已知2 mol氢气完全燃烧生成水蒸气时放出能量484 kJ,且氧气中1 mol O=O键完全断裂时吸收能量496 kJ,
- 在体积都为1L,pH=2的盐酸和醋酸溶液中,投入0.65g锌粒,则下图所示比较符合客观事实的是
- 读某市示意图,回答9~10题。9.下列关于该市功能区分布及规划的说法,正确的是() A.京珠高速公路东侧为老城区、西侧为
- 规范的实验操作是科学探究的基础.下列图示实验操作错误的是()A.倾倒液体 B.取用粉末状固体 C.闻气体气味 D.检查气
- 我国是人民民主专政的社会主义国家,人民是国家的主人。依法实行民主选举、民主决策、民主管理和民主监督,是公民参与政治生活的
- Planninga visit to the UK? Here we help with ways to
- 下列物质能发生消去反应的是( ) A.CH3Br B. C. D.
- 下列物质结构图中,大黑点代表原子序数从1到10的元素的原子实(原子实是原子除去最外层电子后的剩余部分),小黑点代表未用于
- The woundedsoldier died _____I had a chance to know his nam
- Are you able to send a letter with pictures and sounds to so
- 为了解自己的身体情况,健康的小明做了一些测量,其中记录错误的是:( ) A.质量50kg
- 句形转换: 1. It is my first time to be in a plane, so I don’t kn
- 如图, AB⊥ BC ,∠ ABD 的度数比∠ DBC 的度数的两倍少30° ,设 ∠ ABD 和∠ DBC 的度数分别



