初中 数学

-
(1) 从中任取一球,求该球上标记的数字为正数的概率;
-
(2) 从中任取两球,将两球上标记的数字分别记为x、y,求点(x,y)位于第二象限的概率.

 ,-2,+5,1
,-2,+5,1  .并用“<”连接这些数.
.并用“<”连接这些数. ![]()
阅读理解:





①如图13-1,⊙O从⊙O1的位置出发,沿AB滚动到⊙O2的位置,当AB=c时,⊙O恰好自转1周.
②如图13-2,∠ABC相邻的补角是n°,⊙O在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋转的角∠O1BO2 = n°,⊙O在点B处自转  周.
周.
-
(1) 实践应用:
在阅读理解的①中,若AB = 2c , 则⊙O自转周;若AB=1 , 则⊙O自转周.在阅读理解的②中,若∠ABC = 120°,则⊙O在点B处自转周;若∠ABC = 60°,则⊙O在点B处自转周.
-
(2) 如图13-3,∠ABC=90°,AB=BC=
 c . ⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转周.
c . ⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转周.
-
(3) 拓展联想:
如图13-4,△ABC的周长为l , ⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
-
(4) 如图13-5,多边形的周长为l , ⊙O从与某边相切于点D的位置出发,在多边形外部,按顺时针方向沿多边形滚动,又回到与该边相切于点D的位置,直接写出⊙O自转的周数.
 图1
图1  图2
图2
-
(1) 如图1,在BC上找一格点E,连接AE,DE,使得三角形ADE为直角三角形.
-
(2) 如图2,F为BC中点,请在网格中找一格点G,作直线FG,使得FG平分四边形ABCD的面积.


-
(1) △ACD≌△CBE吗?为什么?
-
(2) 小蚂蚁在爬行过程中,DC与BE所成的∠BFC的大小有无变化?请说明理由.

-
(1) 按要求作图:(保留作图痕迹)
①以A为圆心,BC为半径作弧,再以C为圆心,AB为半径作弧,两弧交于点D;
②作出所有以A,B,C,D为顶点的四边形;
-
(2) 比较在(1)中所作出的线段BD与AC的大小关系.
 中,
中,
 ,
,
 ,
,
 ,点
,点
 在线段
在线段
 上,且
上,且
 ,点
,点
 是线段
是线段
 上一动点,连接
上一动点,连接
 ,以
,以
 为圆心、
为圆心、
 的长为半径画弧交线段
的长为半径画弧交线段
 于点
于点
 ,连接
,连接
 ,当
,当
 是
是
 中某条边的
中某条边的
 倍时,求
倍时,求
 的长.小星的探究过程如下:
的长.小星的探究过程如下:

⑴小星分析发现,有三种可能存在的情况,其中,当
 时,通过推理计算可得
时,通过推理计算可得
 的长为
的长为
 .但当他进一步研究其余两种情况时,发现很难通过常规的推理计算得到
.但当他进一步研究其余两种情况时,发现很难通过常规的推理计算得到
 的长,于是尝试利用学习函数的经验解决问题.
的长,于是尝试利用学习函数的经验解决问题.
⑵小星将线段
 的长度记为
的长度记为
 ,
,
 和
和
 的长度分别记为
的长度分别记为
 ,
,
 ,并分别对函数
,并分别对函数
 ,
,
 随着自变量
随着自变量
 的变化规律进行探究.小星通过取点、画图、测量,得到了下表中的几组对应值:
的变化规律进行探究.小星通过取点、画图、测量,得到了下表中的几组对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
①在探究过程中,小星发现当
 时,无须测量可以求出
时,无须测量可以求出
 的长,此时
的长,此时
 的长约为
的长约为
 (结果精确到
(结果精确到
 .参考数据:
.参考数据:
 ).
).
②利用表格中的数据,小星已经在图2所示的平面直角坐标系中画出了
 关于
关于
 的函数图象,请你根据上文中
的函数图象,请你根据上文中
 和
和
 的
的
 组对应值在此平面直角坐标系中描点,并画出
组对应值在此平面直角坐标系中描点,并画出
 关于
关于
 的函数图象
的函数图象
⑶小星发现,想用函数图象彻底解决这个问题,还需要在平面直角坐标系内再画出一个函数的图象,请直接写出这个函数的解析式: , 并在上述平面直角坐标系中画出该函数的图象.
⑷请结合图象直接写出:当
 是
是
 或
或
 的
的
 倍时,
倍时,
 的长约为(结果精确到
的长约为(结果精确到
 ).
).
 中,四边形
中,四边形  和四边形
和四边形  都是正方形,点
都是正方形,点  在
在  轴的正半轴上,点
轴的正半轴上,点  在边
在边  上,反比例函数
上,反比例函数  的图象过点
的图象过点  、
、  .若
.若 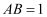 ,则
,则  的值为.
的值为. 

计算:(-1)3-![]() ×[2-(-3)
×[2-(-3)![]() ] .
] .
计算:![]() .
.
化简:(y+2)(y﹣2)﹣(y﹣1)(y+5)
.如果抛物线y=ax2﹣2ax+1经过点A(﹣1,7)、B(x,7),那么x=________.
- 列宁说:“一个民主国家必须承认各地区的自治权,特别是居民的民族成分复杂的地区和专区的自治权,这种自治权同民主集中制一点也
- 下列词语中,各对加点字的读音都不相同的一项是 ( ) A、诽谤/绯红 宫阙/商榷 拙劣/卓
- 从 2009年11月中旬开始,由于全国多个香蕉产区香蕉获得丰收且同时上市,香蕉供过于求,广西香蕉出现严重滞销,其价格跌到
- 请你参加以“亲近书信,传承文化”为主题的语文综合性学习活动。 【活动一:做调查 说现状】下面的调查图表反映了什么情况?请
- 右图为实验室某浓盐酸试剂瓶标签上的有关数据,试根据标签上的有关数据回答下列问题:(1)该浓盐酸的物质的量浓度为
- 一个电容器的规格是“10μF、50V”,则:A.这个电容器加上50V 电压时,电容才是10μFB.这个电容器最大电容量为
- 下列能使植物茎不断长粗的结构是 A.导管
- (8分)如图,OC平分∠BOD,∠AOD=110º,∠COD=35º,求∠AOB的度数.
- 2008年奥运会将在哪个城市举办 A、上海 B、东京 C、北京 D、雅典
- The shop assistant promised me that the material dried easil
- 在平面直角坐标系中,将点P(﹣1,4)向右平移2个单位长度后,再向下平移3个单位长度,得到点P1,则点P1的坐标为
- 某地考核领导干部有新规定,群众投票不满意率达到50%就不称职,不称职者将进行组织调整或降职安排。这反映了我国公民通过()
- 神经系统对内分泌功能的调节有甲、乙、丙三种方式,如右图所示。据图分析回答:(1)若甲模式中,靶腺为甲状腺,则中枢神经系统
- 结合所学知识,说明日本德川幕府实行锁国政策的国际环境,你怎样看待这一政策?
- 在过去很长一段时间里,方便面是消费者的“心头好”。不过,近期有则报道说“方便面卖不动了”。下列做法可以论证这则报道真实有
- 下列能够表示洋葱表皮细胞在发生质壁分离及其复原过程中,液泡体积变化的图形是(注:横坐标代表时间,纵坐标代表液泡体积)
- 最简式相同, 但既不是同系物, 又不是同分异构体的是 A.辛烯和3-甲基-1-丁烯 B.苯和乙炔
- (09年宣武区二模)(14分) 椭圆C的中心坐标为原点O,焦点在y轴上,焦点到相应准线的距离以及离心率均
- Mg、Al组成的混合物与足量盐酸反应,产生标准状况下的氢气4.48L.下列推断中不正确的是() A.参加反应的Mg、Al
- 已知函数在上单调递增,则实数的取值范围是 .
























