初中数学：七年级　 八年级　 九年级　 中考　

初中数学

如图，四边形ABCD中，∠A+∠B=200°，∠ADC、∠DCB的平分线相交于点O，则∠COD的度数是（　　）

A . 110° B . 100° C . 90° D . 80°

先化简，后计算： $\text{[math]}$ ，其中 $\text{[math]}$

计算： $\text{[math]}$

已知 $\text{[math]}$ ， $\text{[math]}$ ，且ab<0，则 $\text{[math]}$ =.

某水果批发商场经销一种水果，如果每千克盈利10元，每天可售出400千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．

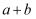（1）当每千克涨价为多少元时，每天的盈利最多？最多是多少？
（2）若商场只要求保证每天的盈利为4420元，同时又可使顾客得到实惠，每千克应涨价为多少元？

抛物线y＝ax²与直线y＝2x－3交于点A(1，b)．

（1）求a，b的值；
（2）求抛物线y＝ax²与直线y＝－2的两个交点B，C的坐标(B点在C点右侧)；
（3）求△OBC的面积．

解下列方程：

（1） x²=3x
（2） 3x²﹣x﹣14=0
（3） $\text{[math]}$ （x+1）²﹣4=0．

如图，在Rt△ABC中，CD是斜边AB上的中线，以CD为直径作⊙O，交BC于点E，过E作EF⊥AB，垂足为F．

（1）求证：直线EF与⊙O相切；
（2）若CE=2，EF=1，求 $\text{[math]}$ 的长．

已知一组数据5，7，9，4，－1，则这组数据的中位数是.

如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t>0）秒。

（1）写出数轴上点B表示的数，点P表示的数（用含t的代数式表示）；
（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？
（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；
（4）若点D是数轴上一点，点D表示的数是x，请你探索式子|x+6|+|x-8|是否有最小值？如果有，直接写出最小值；如果没有，说明理由．

某省植物种类繁多，其中裸子植物的棵数是蕨类植物的 $\text{[math]}$ ，这里是把看作单位“1”。

若4a²﹣2ka+9是一个完全平方式，则k=（）

A . 12 B . ±12 C . ±6 D . 6

为发展乡村经济，某村根据本地特色，创办了山药粉加工厂.该厂需购置一台分装机，计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时，设定分装的标准质量为每袋 $\text{[math]}$ ，与之相差大于 $\text{[math]}$ 为不合格.为检验分装效果，工厂对这两台机器分装的成品进行了抽样和分析，过程如下：

[收集数据]从甲、乙两台机器分装的成品中各随机抽取 $\text{[math]}$ 袋，测得实际质量(单位： $\text{[math]}$ )

如下：

甲： $\text{[math]}$ $\text{[math]}$

乙： $\text{[math]}$ $\text{[math]}$

[整理数据]整理以上数据，得到每袋质量 $\text{[math]}$ 的频数分布表.

[分析数据]根据以上数据，得到以下统计量.

根据以上信息，回答下列问题：

（1）表格中的 $\text{[math]}$ $\text{[math]}$
（2）综合上表中的统计量，判断工厂应选购哪一台分装机，并说明理由.

下列智能手机的功能图标中，既是轴对称图形又是中心对称图形的是( )

A .

B .

C .

D .

下面是“作一个角等于已知角”的尺规作图过程．

已知：∠AOB．

求作：∠A′O′B′，使∠A′O′B′＝∠AOB．

作法：如图，

①画射线O′A′；

②以O为圆心，任意长为半径画弧，交OA于点M，交OB于点N；

③以O′为圆心，OM长为半径画弧，交O′A′于点M′；

④以M′为圆心，MN长为半径画弧，交前弧于点N′；

⑤过N′作射线O′B′，则∠A′O′B′即为所求．

根据上述尺规作图过程，

（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的推理．
∵作图步骤③中，以O′为圆心，OM长为半径画弧，交O′A′于点M′，
∴OM＝ ▲ ．
又∵作图步骤④中，以M′为圆心，MN长为半径画弧，交前弧于点N′，
∴ON＝ ▲ ， MN＝ ▲ ，
∴△MON≌△M′O′N′， ( )（填推理的依据）
∴∠A′O′B′＝∠AOB．