初中 数学
某校八年级以“我最喜爱的体育运动”为主题对该校八年级每位学生进行了调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),经调查每位同学都做了选择,根据调查结果绘制如下统计图表:
某校八年级学生“我最喜爱的体育运动调查情况统计表”
运动项目 | 频数 |
篮球 | 90 |
羽毛球 | m |
乒乓球 | 108 |
跳绳 | 54 |
其它 | n |
请根据以上图表信息解答下列问题:
(1)求该校八年级学生的人数.
(2)求统计表中m、n的值.
(3)求扇形统计图中“乒乓球”所在的扇形的圆心角度数.

-
(1) 计算:
 ;
;
-
(2) 已知
 , 求代数式
, 求代数式 的值;
的值;
-
(3) 先化简,再求值:
 , 其中
, 其中 .
.
如图,在Rt△AOB中,∠AOB=90°,∠BAO=30°,以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.

-
(1) 连接BD,OE.求证:BD=OE;
-
(2) 连接DE交AB于F.求证:F为DE的中点.
已知 是二元一次方程组
是二元一次方程组 的解,则m﹣n的值是 .
的解,则m﹣n的值是 .
 是二元一次方程组
是二元一次方程组 的解,则m﹣n的值是 .
的解,则m﹣n的值是 .
现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
-
(1) 求该快递公司投递总件数的月平均增长率;
-
(2) 如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
下列运算结果正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若一个菱形的一条边长为4cm,则这个菱形的周长为( )
A . 20cm
B . 18cm
C . 16cm
D . 12cm
如图,已知⊙O和点P(点P在⊙O内部),请用直尺和圆规作⊙O的一条弦AB,使得弦AB经过点P且最短(要求不写作法,保留作图痕迹).

如图,在  中,
中,  ,
,  于点
于点  ,
,  于点
于点  ,以点
,以点  为圆心,
为圆心,  为半径作半圆,交
为半径作半圆,交 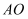 于点
于点  .
.
 中,
中,  ,
,  于点
于点  ,
,  于点
于点  ,以点
,以点  为圆心,
为圆心,  为半径作半圆,交
为半径作半圆,交 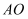 于点
于点  .
.
-
(1) 求证:
 是
是  的切线;
的切线;
-
(2) 若点
 是
是 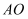 的中点,
的中点,  ,求图中阴影部分的面积;
,求图中阴影部分的面积;
-
(3) 在(2)的条件下,点
 是
是  边上的动点,当
边上的动点,当  取最小值时,直接写出
取最小值时,直接写出  的长.
的长.
已知∠1和∠2互为余角,∠1和∠3互为补角,∠2和∠3的和等于周角的  ,∠则∠1,∠2,∠3的度数分别为( )
,∠则∠1,∠2,∠3的度数分别为( )
 ,∠则∠1,∠2,∠3的度数分别为( )
,∠则∠1,∠2,∠3的度数分别为( )
A . 50°,40°,130°
B . 60°,30°,120°
C . 70°,20°,110°
D . 75°,15°,105°
已知非零实数a.b满足|2a-4|+|b+2|+  +4=2a,则2a+b=.
+4=2a,则2a+b=.
 +4=2a,则2a+b=.
+4=2a,则2a+b=.
矩形的两条对角线的夹角为600 , 较短的边长为6cm,则对角线的长为cm.
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东200米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?(  取1.732,结果精确到1米)
取1.732,结果精确到1米)
 取1.732,结果精确到1米)
取1.732,结果精确到1米) 
在  ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明
ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明  ABD≌
ABD≌  ACD,这个条件可以是(写出一个即可)
ACD,这个条件可以是(写出一个即可)
 ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明
ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明  ABD≌
ABD≌  ACD,这个条件可以是(写出一个即可)
ACD,这个条件可以是(写出一个即可) 
化简下列式子结果为负数的是 



A . 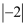 B .
B . 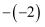 C .
C .  D .
D . 
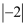 B .
B . 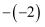 C .
C .  D .
D . 
二元一次方程2x+y=5的正整数解有( )
A . 一组
B . 2组
C . 3组
D . 无数组
在等式x2•(﹣x)•( )=x11中,括号内的代数式为( )
A . x8
B . (﹣x)8
C . ﹣x9
D . ﹣x8
如图,将△ABC置于平面直角坐标系中,点A(-1,3),B(3,1),C(3,3).
(1)请作出△ABC关于原点O的中心对称图形△A’B’C’;(点A的对称点是点A’, 点B的对称点是点B’, 点C的对称点是点C’)
(2)判断以A ,B’,A’ ,B 为顶点的四边形的形状,并直接写出这个四边形的周长.

已知![]() 。
。
若0°<A<90°,且4sin2A-2=0,则∠A=( )
A.30° B.45° C.60° D.75°
最近更新
- 选出加点字的注音全对的一组:( ) A、峥嵘(róng) 百舸(gě) 方遒(qiú) 青荇(xì
- 阅读下面的文字,根据要求作文。 2007年9月28日,祭孔大典在孔子故里曲阜举行,“国人不可不知的五句《论语》经典”征集
- 科技革命使世界发生广泛而深刻的变化,一些国家结合自身条件,抓住机遇,实现了经济的跨越式发展。这是世界经济发展史上的重要经
- (理)已知数列{an}的前n项和为Sn,且满足a1=,an+2SnSn-1=0(n≥2),(1)判断{}是否为等差数列?
- 下列是分析久置于空气中的NaOH固体的相关实验(不考虑水分),其中合理的是序号 实验目的 实验方案 ① 证明变质 取少量
- 如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是() A. 8 B. 10
- 氨气分子空间构型是三角锥形,而甲烷是正四面体形,这是因为A.NH3分子中有一对未成键的孤对电子,它对成键电子的排斥作用较
- 下列物质中都含有氢元素,其中属于酸的是() A.NH3B. CH4C. NaHCO3D. HClO3
- 手机网站传播淫秽色情严重危害青少年身心健康,如果你所在学校的广播站准备发一篇号召同学们远离网络低俗文化的通讯稿,你认为合
- 鉴别与除杂是化学实验的重要内容,下列设计的方案不能达到实验目的的是 选项 实验目的 实验方案 A 鉴别硬水与软水 加入肥
- 填入下面横线处的句子与上下文衔接最恰当的一项是( ) 蜿蜓曲折的沙底小河,顺着山脚涓涓地流着, ________ ,
- “周幽王烽火戏诸侯”、“孔子周游列国”的故事家喻户晓,你知道与“诸侯”、“列国”的产生相关的制度是 A.禅让制
- (6分)阅读下列材料,按要求完成后面提出的问题。材料一:蝙蝠在黑暗中能自由地飞翔,用蜡封住其耳朵,虽然把它放在明亮的房间
- 某位学者认为:世界性的意识形态斗争逐渐减弱,代之而起的将是经济流通、无止境地解决技术问题、环境问题,以及品味微妙的消费者
- I was surprised to know that ________ two top students were
- 如图所示甲中的两个灯泡是________(选填“串联”或“并联”),用乙图中的水流可以类比该电路中的________ (
- 《国际歌》是传遍欧洲、响彻世界的被压迫人民的战歌。要了解其创作背景,应该关注的历史事件是( ) A.英国宪章运动
- 18.阅读下面的材料,根据要求写一篇不少于800字的文章。 在时代发展日益快速的当下,“国学经典与时代追求”这个话题也更
- 如图所示,斜面的倾角为30°,物块A、B通过轻绳连接在弹簧测力计的两端,A、B重力分别为10N、6N,整个装置处于静止状
- (10分)已知地球的平均半径为R,地球自转的角速度为ω,地面上的重力加速度为g.万有引力常量为G。求:(1)地球的质量;



