初中 数学
如图,在平行四边形ABCD中,对角线AC,BD相交于点 O,若BD,AC的和为18 cm,  ,△AOB的周长为13 cm,那么BC的长是( )
,△AOB的周长为13 cm,那么BC的长是( )
 ,△AOB的周长为13 cm,那么BC的长是( )
,△AOB的周长为13 cm,那么BC的长是( )
A . 6 cm
B . 9 cm
C . 3 cm
D . 12 cm
某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为扩大销售增加盈利,尽快减少库存,商场决定采取降价措施,经调查发现,若每件衬衫每降价1元,商场平均每天可以多售出2件.
-
(1) 若每件降价x元,每天盈利y元,求y与x的关系式.
-
(2) 若商场平均每天要盈利1200元,每件衬衫应降价多少元?
-
(3) 每件衬衫降价多少元时,商场每天盈利最多?盈利多少元?
已知某函数的图象过
 ,
,
 两点,下面有四个推断:
两点,下面有四个推断:
 ,
,
 两点,下面有四个推断:
两点,下面有四个推断:
①若此函数的图象为直线,则此函数的图象和直线
 平行;
平行;
②若此函数的图象为双曲线,则此函数的图象分布在第一、三象限;
③若此函数的图象为抛物线,且开口向下,则此函数图象一定与
 轴的负半轴相交;
轴的负半轴相交;
④若此函数的图象为抛物线,且开口向上,则此函数图象对称轴在直线
 左侧。
左侧。
所有合理推断的序号是( )
A . ①③
B . ①④
C . ②③
D . ②④
如图⑴,在△ABC中,∠C=90°,AC=8cm,BC=6cm.
点M由点B出发沿BA方向向点A匀速运动,同时点N由点A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s .连接MN , 设运动时间为t(s)﹙0<t<4﹚,解答下列问题:

-
(1) 设△AMN的面积为S , 求S与t之间的函数关系式,并求出S的最大值;
-
(2) 如图⑵,连接MC , 将△MNC沿NC翻折,得到四边形MNPC , 当四边形MNPC为菱形时,求t的值;
-
(3) 当t的值为,△AMN是等腰三角形.
二次函数y=-(x+2)2+1的顶点坐标为( )
A . (-2,1)
B . (2,1)
C . (2,-1)
D . (-2,-1)
在平面直角坐标系中,直线  过定点C,
过定点C,  (其中
(其中  ),点A在x轴的正半轴上且满足
),点A在x轴的正半轴上且满足  .
.
 过定点C,
过定点C,  (其中
(其中  ),点A在x轴的正半轴上且满足
),点A在x轴的正半轴上且满足  .
.

-
(1) 如图1,直接写出定点C的坐标,直接写出点A的坐标(用含m的式子表示).
-
(2) 如图2,作矩形AOBD,连接CD.
①当
 时,求
时,求  的值.
的值.②是否存在m的值使得
 ?若存在,求出m的值;若不存在,举反例并说明理由.
?若存在,求出m的值;若不存在,举反例并说明理由.
如图,  是边长为
是边长为  的等边三角形,点
的等边三角形,点  、点
、点  的坐标分别为
的坐标分别为 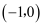 、
、  .第一次将
.第一次将  绕点
绕点  顺时针旋转
顺时针旋转  得到
得到 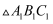 (点
(点  、
、  、
、  的对应点分别是点
的对应点分别是点  、
、 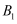 、
、  ,以此类推),第二次仍将
,以此类推),第二次仍将 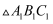 绕点
绕点  顺时针旋转
顺时针旋转  得到
得到  ,……,按此方法进行下去,则点
,……,按此方法进行下去,则点  的坐标为 .
的坐标为 .
 是边长为
是边长为  的等边三角形,点
的等边三角形,点  、点
、点  的坐标分别为
的坐标分别为 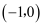 、
、  .第一次将
.第一次将  绕点
绕点  顺时针旋转
顺时针旋转  得到
得到 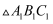 (点
(点  、
、  、
、  的对应点分别是点
的对应点分别是点  、
、 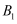 、
、  ,以此类推),第二次仍将
,以此类推),第二次仍将 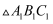 绕点
绕点  顺时针旋转
顺时针旋转  得到
得到  ,……,按此方法进行下去,则点
,……,按此方法进行下去,则点  的坐标为 .
的坐标为 . 
某玩具车间每天能生产甲种玩具零件100个或乙种玩具零件200个,甲种玩具零件1个与乙种玩具零件2个能组成一个完整的玩具,怎样安排生产才能在30天内组装出最多的玩具?设生产甲种玩具零件x天,生产乙种玩具零件y天,则有( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
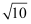 的整数部分,
的整数部分,
已知∠α=76°,∠β=41°31′,求:
-
(1) ∠β的余角;
-
(2) ∠α的2倍与∠β的
 的差.
的差.
如图是某旅行车旅客携带行李收费示意图,小李所携带的行李重20千克,那么小李应该交费(元).

计算:  .
.
 .
.
某超市销售一种饮料,每瓶进价为6元.当每瓶售价为10元时,日均销售量为160瓶.经市场调查表明,每瓶售价每增加0.5元,日均销售量减少10瓶.
-
(1) 当每瓶售价为11元时,日均销售量为瓶;
-
(2) 当每瓶售价为多少元时,所得日均总利润为700元?
-
(3) 当每瓶售价为多少元时,所得日均总利润最大?最大日均总利润为多少元?
若点M(1-m,2+m)在第四象限内,则m的取值范围是.
一个正数  的两个不同的平方根分别是
的两个不同的平方根分别是 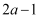 和
和  .
.
 的两个不同的平方根分别是
的两个不同的平方根分别是 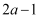 和
和  .
.
-
(1) 求
 和
和  的值;
的值;
-
(2) 求
 的平方根.
的平方根.
若 、
、 、
、 为一个三角形的三边长,则式子
为一个三角形的三边长,则式子 的值( )
的值( )
 、
、 、
、 为一个三角形的三边长,则式子
为一个三角形的三边长,则式子 的值( )
的值( )
A . 一定为正数
B . 一定为负数
C . 可能是正数,也可能是负数
D . 可能为0
已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD.

-
(1) 求证:△AGE≌△DAC;
-
(2) 过E做EF∥DC.交BC于F.连接AF.判断△AEF是怎样的三角形.并证明你的结论.
下列常见的手机软件图标中,是轴对称图形的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下面四个图形中,∠1=∠2一定成立的是( )
A .  B .
B .  C .
C .  D .
D . 
 C .
C .  D .
D . 
化简:2(a+1) -a=
最近更新
- (2011内蒙古乌兰察布,1,3分)4 的平方根是( )A.2B.16C.±2D.±16
- 如图所示,半径和动能都相等的两个小球相向而行.甲球质量m甲大于乙球质量m乙,水平面是光滑的,两球做对心碰撞以后的运动情况
- You are not in good health, I think. You could improve your
- I haddressed quite nicely for my first day as a student at S
- 分析下列各图,正确的是()A.图甲由于单侧光照的影响,胚芽鞘将向光弯曲生长 B.图乙茎卷须中生长素含量外侧比内侧多,所以
- .方程,当时,m的取值范围是( )A.B.C.D.
- 构建模式图,探究地理基本原理、过程、成因及规律,是学习地理的方法之一。读下图,回答21-22题。21.如果该图为大
- 我国“西气东输”一线工程主干管道没有经过的地形区( ) A.青藏高原 B.黄土高原
- 第二节 读写任务(共1小题,满分25分) 阅读下面的短文,然后按照要求写一篇150词左右的英语短文。 In moder
- 除去下列物质中少量杂质的方法正确的是 ( ) A.除去
- 下列叙述中不正确的是( )A.钠原子有强还原性,钠离子有弱氧化性 B.若电解熔融的氯化钠,则钠离子被还原成钠原子
- —Waiter! —______? —I can’t eat this.It’s too salty. A.Yes, s
- (本题满分15分)已知a∈R,函数f (x) =x3 + ax2 + 2ax (x∈R). (Ⅰ)当a = 1
- (5分)已知水平地面上有两个相距为S的地震观察点A和B,观察到地下O处发生地震后(地面下H深度),发出的纵波和横波到达观
- 每年的5月13日是世界无烟日。香烟的成分很复杂,燃烧产生的烟气中含有许多强致癌物质和有害物质,其中对人体危害最大的分别是
- Some people got sick ________ the cold weather. A
- 从公元前490年到公元前322年,雅典大约有一半左右的政治家(包括伯利克里)都不同程度地受到群众惩罚,大部分控告的起因只
- 如图,在△中,,是边上的一点,,,,则的长为_____________.
- 函数的定义域为开区间,导函数在内的图象如图所示,则函数在开区间内有极小值点( ) A.个 B.个 C.个
- 上海世博会曾吸引了大批海内外人士利用各种交通工具前往参观。然而在19世纪70年代,江苏沿江居民到上海,最有可能乘坐的下列



